Elementos de un círculo

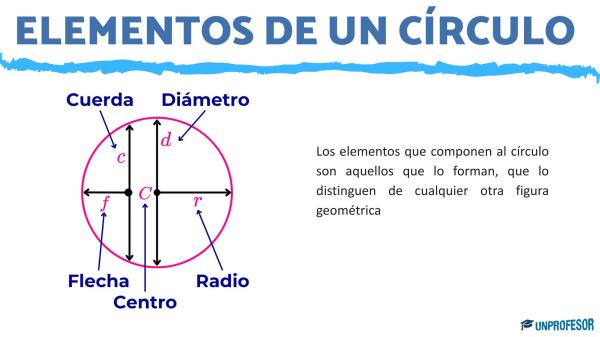
Los elementos que forman al círculo son los siguientes:

1. CENTRO: el centro de todo círculo es el punto interior de la circunferencia, es decir el punto central del círculo. Es el origen del círculo, y se encuentra a la misma distancia de cada uno de los puntos que forman la circunferencia que lo contiene.
2. DIÁMETRO: el diámetro de un círculo es la longitud más grande que existe dentro del mismo, comenzando desde uno de los puntos que forman la circunferencia que lo delimita, hasta otro de los puntos de la circunferencia pero siempre pasando por el centro. Es decir, es un segmento de recta que atraviesa el origen del círculo, y termina en dos puntos de la circunferencia, se escribe con la letra d o D y es igual al doble del radio. El diámetro de cualquier círculo, divide a este, en dos mitades iguales llamadas semicircunferencias.
3. RADIO: el radio de un círculo es aquella recta que tiene su origen en el centro del círculo y termina en uno de los puntos de la circunferencia que lo contiene. Es decir, que el radio es la mitad de un diámetro y se escribe con la letra r o R. Dentro de cada círculo, existen infinitos radios, ya que los puntos que forman la circunferencia son infinitos, y todos ellos miden la misma longitud.
4. CUERDA: la cuerda es aquel segmento de recta que se parece al radio, pero no siempre mide lo mismo, ya que comienza en cualquier punto de la circunferencia y termina en otro, sin necesariamente pasar por el centro. La cuerda dentro de un círculo puede ser menor o mayor en longitud que el radio, pero siempre será menor que la longitud del diámetro.
5. FLECHA: la flecha es aquel segmento de recta que tiene su origen en el punto medio de una cuerda cualquiera de manera perpendicular a ella. Se forma de esta manera, una línea que comienza en la cuerda y termina en un punto de la circunferencia.
6. SEMICIRCUNFERENCIA: la semicircunferencia de un círculo es aquella que se forma a partir del diámetro, es decir que este divide al círculo en dos mitades iguales. La semicircunferencia es el arco que paso mayor medida en cualquier círculo.
7. ARCO: el arco de un círculo es aquella parte del mismo que se genera a partir de dos puntos que forman parte de la circunferencia. Es decir, es aquella porción que se forma cuando se eligen dos puntos del contorno del círculo. El arco que se forma con el diámetro, llamado semicircunferencia es siempre el que tiene mayor longitud.

El cálculo de la circunferencia de un círculo tiene diferentes aplicaciones, ya que esta cuenta nos revela cuál es el perímetro del círculo en cuestión. Es sumamente importante en la vida cotidiana debido a que se pueden calcular materiales necesarios, distancias que se recorren y hasta cálculos más complejos dentro de la ingeniería.

Podemos calcular la circunferencia de un círculo con una fórmula muy sencilla que relaciona el diámetro o radio con el número irracional π. Es decir, que debemos conocer un dato, el radio o el diámetro del círculo, para poder conocer su perímetro.

La fórmula que se utiliza para ello es: Perímetro de un círculo = π . d = π . 2 . r

Como ya mencionamos, la d se refiere al diámetro del círculo. Y como sabemos que el diámetro es igual al doble del radio, entonces también podemos utilizarlo para calcularlo, siendo r el radio.

Ejemplo

Queremos calcular la circunferencia de un círculo de diámetro 12 cm.

Solución: utilizaremos la fórmula para calcularlo. Sabemos que el diámetro es igual a 12 cm por lo tanto el radio es 6 cm. Vamos a comprobar con ambas fórmulas que el resultado es el mismo.

• Perímetro de un círculo = π . d = π . 12 cm = 37,7 cm
• Perímetro de un círculo = π . 2 . r = π . 2 . 6 cm = 37,7 cm

Entonces el perímetro de un círculo de diámetro 12 cm es igual a 37,7 cm.

Aquí te dejamos un vídeo de nuestra profesora de matemáticas sobre la circunferencia y el círculo:

En matemáticas, el círculo es una de las figuras geométricas más utilizadas, ya que tiene diferentes usos en la vida cotidiana y además como mencionamos anteriormente, se utiliza para crear otras figuras nuevas.

Cuando hablamos de círculo, debemos recordar que podemos pensarlo desde dos perspectivas, la de su parte interior, llamada específicamente círculo, pero también su contorno, llamada circunferencia.

El círculo, como mencionamos anteriormente, es la figura geométrica más básica que puede también formar otras figuras geométricas. Los círculos están formados por una línea curva y cerrada, que posee infinitos puntos en su composición, y no tiene ni vértices ni aristas.

De vez en cuando, se trazan rectas que intersecan o tocan en un solo punto al círculo para poder hallar o saber las medidas de los ángulos interiores, pero aún así, estas líneas rectas NO forman parte del círculo.

En esta otra lección te descubrimos las diferencias entre circunferencia y círculo.

Si deseas leer más artículos parecidos a Elementos de un círculo, te recomendamos que entres en nuestra categoría de Geometría.