La circunferencia y el círculo para niños

La circunferencia es una de las figuras geométricas más conocidas y utilizadas en matemáticas. Consiste en una curva cerrada que tiene como característica principal que todos los puntos que la forman se encuentran a la misma distancia de otro punto llamado centro. Es decir, todos los puntos que forman la circunferencia son equidistantes del punto central.

Las figuras geométricas que llamamos polígonos tienen la diferencia con la circunferencia de que todas, a pesar de que también son figuras cerradas, están formadas por líneas rectas, mientras que la circunferencia se forma con una línea curva.

Entonces, la circunferencia es una línea curva cerrada que posee un centro, el cual se encuentra a la misma distancia de todos los puntos que la forman.

El círculo es la figura geométrica delimitada por una circunferencia o, dicho de una forma más sencilla, es la superficie del interior de la circunferencia. Algunos ejemplos son las monedas y las pizzas.

Como ves, existe una diferencia entre circunferencia y círculo. Mientras que la circunferencia es la línea curva que delimita la figura, el círculo es el interior de la misma.

Existen algunos elementos que componen a la circunferencia y el interior de la misma, que ya sabemos se llama círculo. Son los siguientes:

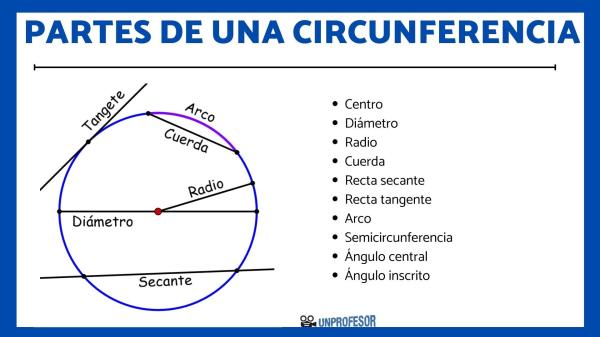
• Diámetro: el diámetro de una circunferencia es aquella línea recta que conecta dos puntos de la misma, pasando siempre por el centro. Todos los puntos que se unen de esta forma en una circunferencia, tienen la misma medida denominada diámetro.
• Centro: el centro de una circunferencia es aquel punto interior que se encuentra a la misma distancia de cada uno de los puntos de la misma.
• Radio: el radio de una circunferencia es aquella línea recta que une un punto cualquiera de la circunferencia con el centro de la misma. Todos los puntos que se unen de esta forma, tienen la misma medida denominada radio.
• Cuerda: la cuerda de una circunferencia es aquella línea recta que une dos puntos de una circunferencia sin pasar por el centro. Es decir, aquellas líneas que NO son como el diámetro, ya que no posee la misma medida y no pasan por el punto central.
• Sector circular: el sector circular de una circunferencia es aquella porción que se logra a partir de dos radios y ese tramo de la circunferencia que los delimita.
• Arco: el arco de una circunferencia se sitúa entre dos puntos de corte de una cuerda con la propia circunferencia.

Los elementos de un círculo son:

• Centro: punto interior de la circunferencia. Esto quiere decir que el origen se encuentra a la misma distancia en todos los puntos de la circunferencia que lo delimita.
• Semicircunferencia: mitad de una circunferencia. Se puede considerar como el arco de mayor tamaño de cualquier círculo. Aquí te contamos cómo calcular el perímetro de una semicircunferencia.
• Radio: segmento de recta que comienza en el centro de la circunferencia y va hacia cualquier punto de la circunferencia. Se representa con la letra r y son infinitos dentro de la circunferencia. El radio de cada círculo mide siempre lo mismo en cualquiera de sus puntos y es equivalente a la mitad del diámetro. Es decir, que el diámetro es igual a dos veces el radio.
• Diámetro: segmento de recta que comienza desde uno de los puntos del perímetro hacia otro punto del mismo, pasando siempre por el centro de la circunferencia. El diámetro se representa con la letra d, y equivale a dos veces el radio. El diámetro divide a una circunferencia en dos semicircunferencias iguales, es decir el círculo en dos mitades. El diámetro es la cuerda que posee mayor longitud dentro de un círculo. Aquí te contamos cómo sacar el diámetro de un círculo.
• Cuerda: segmento de recta que comienza desde uno de los puntos del perímetro hacia otro del mismo, pero en esta ocasión NO pasa por el centro del círculo, y por lo tanto NO es el diámetro, sino que es un segmento con menor longitud que este. Con esto podemos asegurar que una cuerda siempre tendrá menor longitud que el diámetro.
• Flecha: segmento de recta que comienza desde el punto medio de una cuerda cualquiera, y es perpendicular a ésta formando una línea que parte de la cuerda y llega hasta el perímetro.
• Arco: porción de una circunferencia que está ubicada entre dos puntos pertenecientes a esta. Los arcos pueden originarse a partir de los radios, cuerdas y hasta elementos cualquiera. Cuando el tamaño de un arco se corresponde con el diámetro, entonces el arco es una semicircunferencia.

Vamos a descubrirte las diferentes posiciones que pueden tener las circunferencias.

Posición de rectas con respecto a una circunferencia

Una recta y una circunferencia pueden tener diferentes posiciones, y estas son:

• Exterior: una recta exterior a una circunferencia es aquella que no toca ni interseca a la circunferencia en ninguno de sus puntos. Es decir, se encuentra en el exterior de la misma.
• Secante: una recta secante a una circunferencia es aquella que interseca a la circunferencia en dos puntos cualesquiera. Es decir, que atraviesa a la circunferencia en dos puntos.
• Tangente: una recta tangente a una circunferencia es aquella que toca a la misma es uno solo de sus puntos. Es decir, a simple vista parece una recta exterior, pero se une a la circunferencia en uno de sus puntos.

Posición de dos circunferencias

Dos circunferencias pueden posicionarse de diferentes formas y estas son:

• Exteriores: dos circunferencias son exteriores si están ubicadas de forma tal que no se toquen ninguno de todos sus puntos.
• Tangentes: dos circunferencias son tangentes si están ubicadas de forma tal que sólo uno de sus puntos se tocan.
• Secantes: dos circunferencias son secantes si se intersecan en dos de sus puntos, es decir que están atravesadas una con la otra.
• Interiores: hablamos de circunferencias interiores cuando una de ellas, está completamente dentro de la segunda. Es decir, que una de las mismas contiene a la otra.

Cuando hablamos de longitud de una circunferencia, nos estamos refiriendo a la medida de la línea curva que la forma. Es decir, queremos calcular la longitud que delimita al círculo.

Para ello, existe una fórmula que resulta muy fácil de utilizar para calcularlo. Teniendo en cuenta el número irracional π (pi), calculamos:

Longitud de una circunferencia = 2 x π x r

Siendo r el radio de la circunferencia. Así mismo, sabiendo que el diámetro es igual a la suma de dos radios, podemos escribir la fórmula como:

Longitud de una circunferencia = π x d

Siendo d el diámetro.

Ejemplo

Veamos un ejemplo. Queremos calcular la longitud de la circunferencia que posee un radio de 12 cm. Entonces:

Longitud de una circunferencia = 2 x π x r = 2 x π x 12 cm = 75.4 cm

La longitud de una circunferencia de radio 12 cm es igual a 75.4 cm.

Si queremos calcular la longitud de una circunferencia de diámetro 18 cm, entonces utilizamos la segunda fórmula y encontramos el valor.

Longitud de una circunferencia = π x d = π x 18 cm = 56.5 cm

La longitud de una circunferencia de 18 cm de diámetro es de 56.5 cm.

Descubre las partes de la circunferencia.

La diferencia que existe entre circunferencia y círculo ya la mencionamos muchas veces antes. La circunferencia es el perímetro del círculo, mientras que el círculo es la superficie contenida en la circunferencia.

La diferencia se nota claramente en las definiciones de ambos conceptos. La circunferencia es una curva cerrada que delimita al círculo, y el círculo es la superficie que existe dentro de una circunferencia.

Para calcular la circunferencia de un círculo, debemos calcular su perímetro. Existe una fórmula sencilla que se utiliza para calcular el perímetro de cualquier circunferencia, sabiendo solamente la longitud del diámetro o del radio. La fórmula es la siguiente:

Circunferencia de un círculo = π . d = π . 2 . r

Siendo d: diámetro y r: radio. Como sabemos que un diámetro es equivalente a dos radios, también podemos utilizar la fórmula con la longitud del radio multiplicada por dos. El valor de π, es aprox. ya que es un número irracional, cuyos decimales infinitos no se conocen todos.

Realizar los siguientes ejercicios, y luego comprobar sus soluciones.

1. Calcular la circunferencia de un círculo de diámetro 12 cm.
2. Calcular la circunferencia de un círculo de radio 8 cm.
3. Calcular el diámetro de un círculo cuya circunferencia mide aprox. 40,8407 cm.

Soluciones

1- Calcular la circunferencia de un círculo de diámetro 12 cm. Utilizamos la fórmula que tiene el valor del diámetro, entonces:

Circunferencia de un círculo = π . d = π . 12 cm = 37,699 cm

Por lo tanto, la circunferencia del círculo de 12 cm de diámetro es igual a 37,699 cm.

2- Calcular la circunferencia de un círculo de radio 8 cm. Utilizamos la fórmula que tiene el valor del radio, entonces:

Circunferencia de un círculo = π . 2 . r = π . 2 . 8 cm = 50,265 cm

Por lo tanto, la circunferencia del círculo de 8 cm de radio es igual a 50,265 cm.

3- Calcular el diámetro de un círculo cuya circunferencia mide aprox. 40,8407 cm. En este caso, tenemos el valor del resultado de la circunferencia, pero queremos saber el valor del diámetro del círculo, entonces vamos a utilizar la fórmula con el diámetro y a despejar el valor.

Circunferencia de un círculo = π . d = 40,8407 cm

d = 40,8407 cm / π

d = 13 cm

Por lo tanto, la circunferencia que mide 40,8407 corresponde a un círculo de diámetro 13 cm.

Si deseas leer más artículos parecidos a La circunferencia y el círculo para niños, te recomendamos que entres en nuestra categoría de Geometría.