Cuáles son las razones trigonométricas

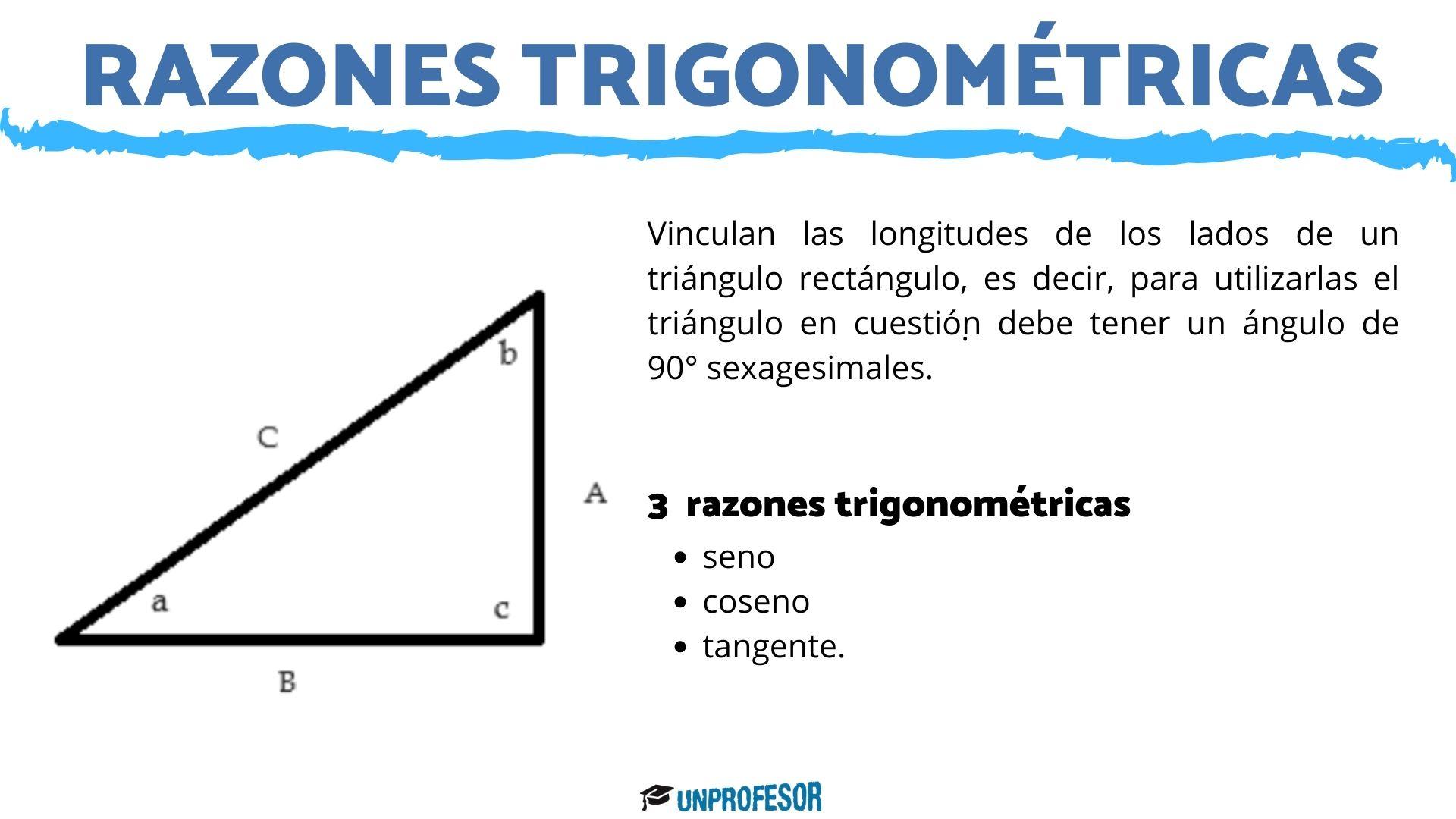
Las razones trigonométricas vinculan las longitudes de los lados de un triángulo rectángulo, es decir, para utilizarlas el triángulo en cuestión debe tener un ángulo de 90° sexagesimales.

La forma de vincular estas razones está definida como el cociente o división entre dos de los lados de un triángulo rectángulo asociado a uno de los ángulos que NO es el de 90° sexagesimales.

Se denominan razones trigonométricas justamente porque establece una razón entre las longitudes de los lados y un ángulo.

Existen tres razones trigonométricas fundamentales que son:

1. seno
2. coseno
3. tangente.

Recordemos que para utilizar el teorema de Pitágoras, el triángulo debía ser uno que tuviera un ángulo de 90° sexagesimales. El lado opuesto al ángulo recto se denomina hipotenusa mientras que los lados que forman ese ángulo se llaman catetos.

Tenemos un triángulo rectángulo con uno de sus ángulos, diferentes al recto, llamado ∝. Las fórmulas de las razones trigonométricas fundamentales que se relacionan con el triángulo rectángulo son:

• sen ∝ = cateto opuesto / hipotenusa
• cos ∝ = cateto adyacente / hipotenusa
• tg ∝ = cateto opuesto / cateto adyacente

Para recordar estas razones se puede utilizar una regla mnemotécnica, que es una oración fácil de recordar para no olvidar cuáles son estas reglas.

• SOHCAHTOA es la palabra que vamos a utilizar, y debemos recordar que se divide en tres letras.
• SOH será el Seno del ángulo es igual al cateto Opuesto dividido la Hipotenusa
• CAH será el Coseno del ángulo es igual al cateto Adyacente dividido la Hipotenusa
• TOA será la Tangente del ángulo es igual al cateto Opuesto dividido el cateto Adyacente

Ahora bien, vamos a pensar en un triángulo ABC (ver imagen adjunta en el apartado), con ángulo a, b y c, donde el c es el que mide 90° sexagesimales. Sabemos que el lado C será la hipotenusa, mientras que A y B serán los catetos.

Tomamos primero el ángulo a para establecer las razones trigonométricas.

Sen a = cateto opuesto / hipotenusa = A / C

El cateto opuesto al ángulo a se refiere al lado que se encuentra “opuesto” o enfrente del ángulo en cuestión.

Cos a = cateto adyacente / hipotenusa = B / C

El cateto adyacente al ángulo nos indica que el lado “forma” al ángulo en cuestión, siendo el cateto diferente a la hipotenusa.

Tg a = cateto opuesto / cateto adyacente = A / B

Los dos catetos que ya habíamos mencionado anteriormente.

Si en cambio tomamos el ángulo b, las razones trigonométricas cambian, porque los catetos opuestos y adyacentes no serán los mismos con respecto al ángulo anteriormente elegido.

• Sen b = cateto opuesto / hipotenusa = B / C
• Cos b = cateto adyacente / hipotenusa = A / C
• Tg b = cateto opuesto / cateto adyacente = B / A

Pensemos en un triángulo rectángulo cuyas medidas de dos de sus lados son A = 20 cm, B = 40 cm, y C que no sabemos aún cuánto mide. La medida del ángulo a= 30°. Averiguaremos las medidas de los ángulos y lados faltantes. (Ver imagen adjunta al apartado)

En este caso el lado B será la hipotenusa del triángulo. Y recordemos que la suma de los tres ángulos interiores de un triángulo es siempre 180° sexagesimales, por lo que podemos buscar el ángulo faltante a con ese dato.

• a + b + c = 180°
• a + 90° + 30° = 180°
• a = 180° - 90° - 30°
• a = 60°

Ahora utilizaremos las razones trigonométricas para averiguar el valor del lado faltante C.

Usamos la regla mnemotécnica SOHCAHTOA con el ángulo c.

Como necesitamos obtener el valor del lado C que resulta ser el cateto opuesto al ángulo c, y conocemos el valor de la hipotenusa, entonces utilizaremos la razón del seno.

• Sen c = cateto opuesto / hipotenusa
• Sen 30° = C / 40 cm
• Sen 30° x 40 cm = C
• 20 cm = C

Si en cambio utilizamos el ángulo a = 60° que hallamos al principio, podemos utilizar la razón del coseno.

Cos a = cateto adyacente / hipotenusa

• Cos 60° = C / B
• Cos 60° = C / 40 cm
• Cos 60° x 40 cm = C
• 20 cm = C

Obtenemos así, el mismo resultado.

Si deseas leer más artículos parecidos a Cuáles son las razones trigonométricas, te recomendamos que entres en nuestra categoría de Trigonometría.