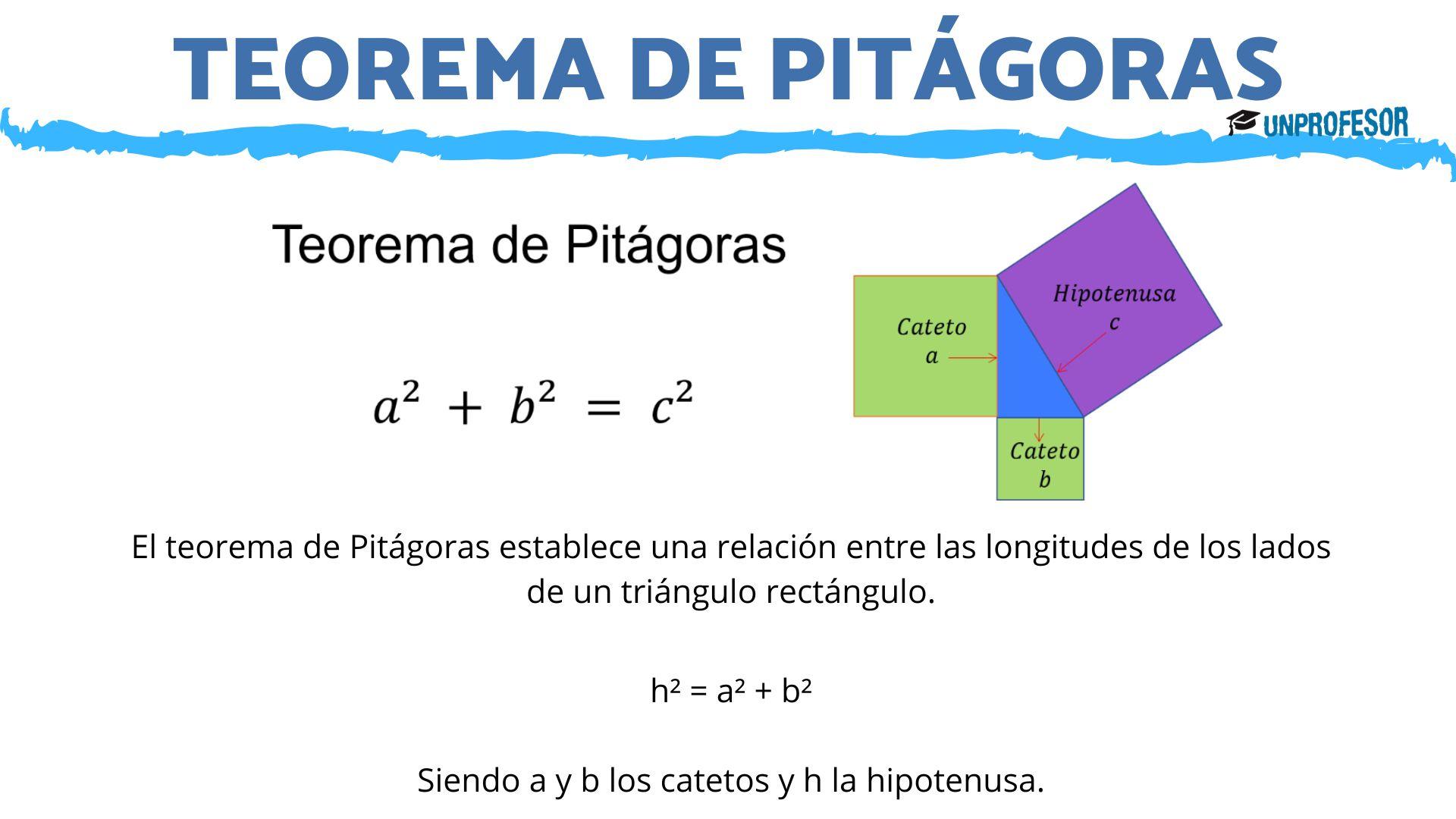
Teorema de Pitágoras


El teorema de Pitágoras establece una relación entre las longitudes de los lados de un triángulo rectángulo. En la lección de hoy de unProfesor estudiaremos qué es el teorema de Pitágoras, sus aplicaciones y enunciado. Veremos algunos ejemplos, y terminaremos con ejercicios resueltos para comprenderlo.
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
¿Qué es el teorema de Pitágoras?
El teorema que hoy presentamos es un enunciado matemático que realizó Pitágoras hace muchos años, incluso antes de Cristo. Este matemático realizó aportes que son muy importantes hasta la fecha, en geometría y aritmética. Es uno de los teoremas más utilizados e importantes de la matemática y tiene la mayor cantidad de demostraciones realizadas.
Teorema de Pitágoras: enunciado
En un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
h² = a² + b²
Siendo a y b los catetos y h la hipotenusa.
Los triángulos rectángulos poseen un ángulo que mide 90° sexagesimales. El lado opuesto a este ángulo se denomina hipotenusa, mientras que los lados que forman el ángulo recto, se llaman catetos.
La hipotenusa es el lado que posee mayor longitud en todos los triángulos rectángulos.

Aplicaciones del teorema de Pitágoras
El teorema de Pitágoras, en matemáticas, suele utilizarse para conocer el lado faltante de un triángulo rectángulo, es decir en un ejercicio se darán a conocer los valores de las longitudes de dos de sus lados, y el tercero se hallará utilizando el teorema en cuestión.
Pero en la vida diaria, este teorema se utiliza para calcular distancias, áreas, dimensiones, alturas, etc. Esto quiere decir, que disciplinas como química, física, ingeniería y construcción lo utilizan.
De acuerdo a la medida faltante, puede haber dos opciones para resolverlo, por un lado puede faltar la hipotenusa y por otro uno de los cateto
Hipotenusa
Si tenemos un triángulo rectángulo y queremos calcular el valor faltante de la longitud de la hipotenusa, utilizamos el teorema de Pitágoras para resolverlo de la siguiente forma:
- h² = a² + b²
- despejamos h para conocer su valor
- h = raiz(a² + b²)
Por ejemplo: tenemos un triángulo rectángulo cuya medidas de sus catetos son: a = 5 cm y b = 6 cm, calcular la medida de la hipotenusa.
Entonces, utilizamos el teorema de Pitágoras para ello.
- h² = a² + b²
- despejamos h para conocer su valor
- h² = 5² + 6²
- h = raiz(25 + 36)
- h = 7,81
- Por lo tanto, la medida de la hipotenusa es 7,81 cm.
Catetos
Si tenemos un triángulo rectángulo y queremos calcular el valor faltante de la longitud de uno de sus catetos, utilizamos el teorema de Pitágoras para resolverlo de la siguiente forma:
- h² = a² + b²
- (utilizamos b en este ejemplo)
- h² - a² = b²
- despejamos b para conocer su valor
- raíz(h² - a²) = b
Por ejemplo: tenemos un triángulo rectángulo con h = 5 cm y su cateto a = 3 cm, calcular la medida del cateto faltante.
Utilizamos el teorema:
- h² = a² + b²
- 5² - 3² = b²
- despejamos b para conocer su valor
- raíz(25 - 9) = b
- raíz(16) = b
- 4 = b
Por lo tanto, la medida del cateto b es 4 cm.

Problemas con teorema de Pitágoras
Aquí te dejamos problemas resueltos con el teorema de Pitágoras para que puedas practicar en casa.
- Una escalera de 3 m está apoyada sobre una pared. La misma está apoyada sobre el suelo a 1 m de la pared, calcula la altura que alcanza.
- La sombra de un árbol proyectada es de 2 m, y la distancia desde la punta del mismo hasta la parte más alejada de la sombra es de 4 m. Calcular la altura del árbol.
- Desde lo más alto de un edificio de 45 m se observa a una persona que se encuentra a 200 m desde ese punto. ¿A qué distancia del suelo se encuentran separados?
- Un tobogán tiene de altura 2.5 m del suelo, la distancia desde allí hasta el final del recorrido es de 6 m. Calcular el recorrido del tobogán.
Soluciones
1- La pared y el suelo forman un ángulo de 90° sexagesimales, por lo que junto con la escalera forman un triángulo rectángulo. Utilizando el teorema de Pitágoras, podemos decir que la escalera será la hipotenusa, mientras que la pared y el suelo los catetos.
Entonces h = 3 m, y a = 1m.
Calculamos
h² = a² + b²
3² - 1² = b²
despejamos b para conocer su valor
raíz(9 - 1) = b
raíz(8) = b
2,82 = b
Por lo tanto la escalera alcanza una altura de 2,82 m del suelo.
2- El árbol y la sombra del mismo forman un ángulo de 90° sexagesimales, por lo tanto junto con la distancia que buscamos averiguar se forma un triángulo rectángulo. En este caso, la distancia faltante es la hipotenusa, mientras que el árbol y la sombra son los catetos.
Entonces a = 2 m y b = 4m.
Calculamos
h² = a² + b²
h² = 2² + 4²
h = raiz(4 + 16)
h = 4,47
Por lo tanto, la distancia entre la sombra y la punta del árbol es de 4,47 cm.
3-El edificio y el suelo forman un ángulo de 90° sexagesimales, por lo tanto junto con la distancia donde se lo observa forman un triángulo rectángulo. En este problema, esa distancia es la hipotenusa mientras que lo alto del edificio es uno de los catetos.
Entonces h = 200 m y a = 45 m.
Calculamos
h² = a² + b²
200² - 45² = b²
raíz(40000 - 2025) = b
194,87 = b
Por lo tanto la distancia es de 194,87 m.
4- La altura del tobogán junto con la distancia del final en el suelo forman un ángulo de 90° sexagesimales, junto con el recorrido del mismo hacen un triángulo rectángulo. En este caso el recorrido será la hipotenusa a averiguar, mientras que la altura y distancia son los catetos.
Entonces a = 2.5 m y b = 6 m.
Calculamos
h² = a² + b²
h² = 2.5² + 6²
h = raiz(6.25 + 36)
h = 6,5
Por lo tanto, la distancia recorrida del tobogán es de 6,5 m.
Si deseas leer más artículos parecidos a Teorema de Pitágoras, te recomendamos que entres en nuestra categoría de Trigonometría.