Qué es la radicación y sus propiedades - con ejemplos

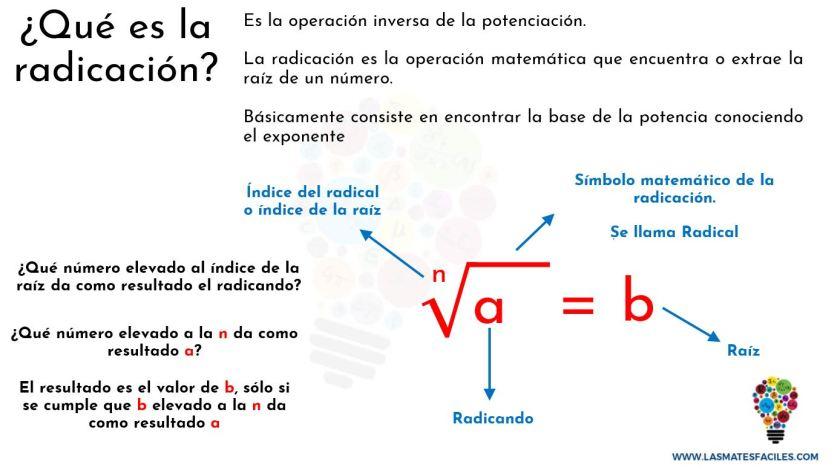
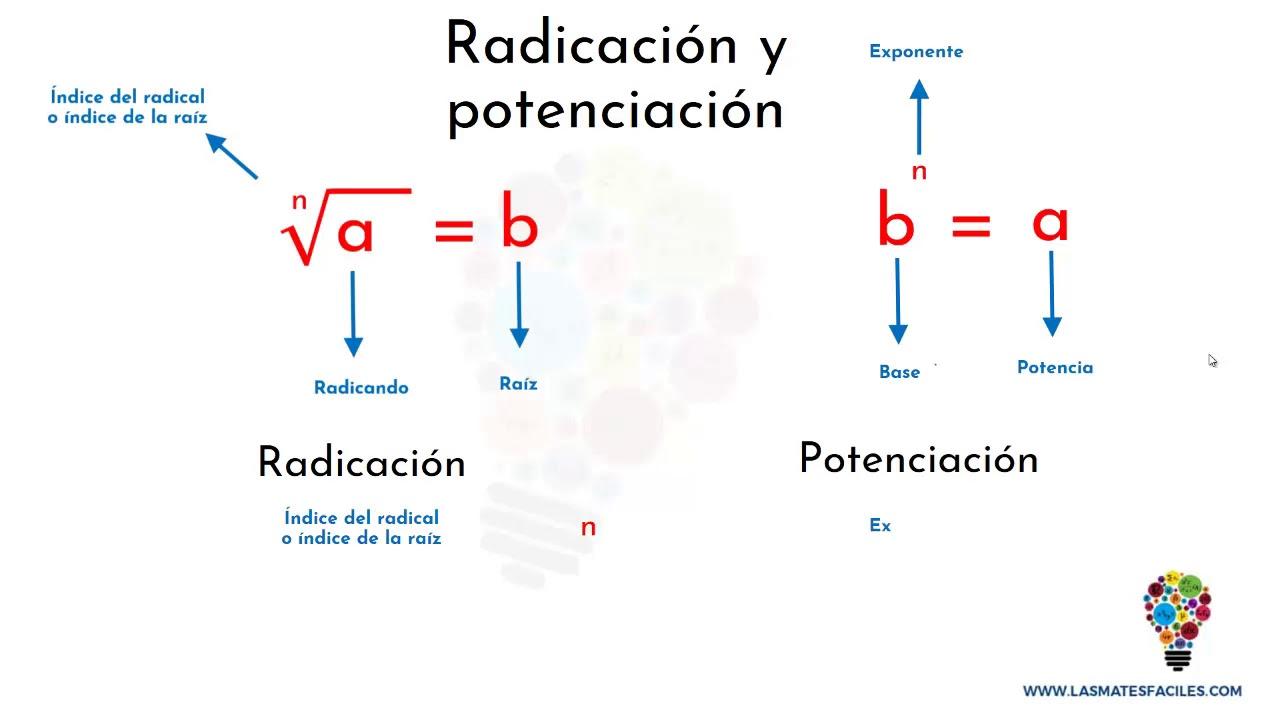
La radicación es una operación matemática que podemos catalogar como la opuesta a la potenciación. Es decir, radicar es lo contrario a elevar a un número entero.

Identificamos la radicación en tanto que se escribe de una manera característica: encontramos el índice, el radicando y la raíz. De este modo, si tenemos √25 = 5, el radicando es 25 y la raíz 5, pero el índice es 2.

¿Cómo identificamos el índice?

Pues es muy sencillo, si no tenemos ningún número, el índice será 2. Si no es 2, tendremos escrito un pequeño número encima del símbolo de radicación, como por ejemplo: ∛8 = 2, en la que el índice es 3.

La raíz cuadrada es, sin duda, la forma más común de radicación, y se utiliza frecuentemente en diversos campos como la ingeniería y las ciencias. Además, la comprensión de la radicación es esencial para estudios avanzados en álgebra y cálculo.

Imagen: Mates fáciles

Una vez que ya sabemos qué es la radicación, vamos a ver cuáles son sus propiedades:

1. Se resuelve encontrando el número que, multiplicado por sí mismo el número de veces que dice el índice, da el radicando. Por eso, ∛8 = 2, ya que 2 x 2 x 2 = 8.
2. El radicando puede ser negativo en los radicales con índice impar, pero no en los radicales con índice par. Así pues, ∛-27 = -3, pero √-9 no tiene solución.
3. El resultado o raíz de los radicales con índice par, se debe dar con una doble solución, pues puede ser negativo o positivo. Pensemos que, por ejemplo, √25 puede resolverse tanto multiplicando 5 x 5 como multiplicando (-5) x (-5). De este modo, la respuesta a √25 es ±5 o, lo que es lo mismo, 5 y -5.
4. La multiplicación de dos radicales con el mismo índice se realiza multiplicando los radicandos y manteniendo el índice. Por ejemplo: √3 * √8 = √24. Otro ejemplo sería: ∜9 * ∜2 = ∜18.
5. Lo mismo sucede con las divisiones, si tienen el mismo índice, se dividen los radicandos: (√12)/(√4) = √3. Otro ejemplo podría ser (∜25) / (∜5) = ∜5.

Es importante recordar que, en situaciones prácticas, las propiedades de la radicación son útiles en simplificaciones matemáticas y en la resolución de ecuaciones. Asimismo, en la ciencia, estas propiedades se aplican en cálculos de ondas y fenómenos físicos.

Por otro lado, el dominio de estas propiedades permite una mayor flexibilidad en la manipulación de expresiones algebraicas, facilitando la resolución de problemas más complejos.

Los ejemplos más comunes son los de las raíces cuadradas, es decir, las raíces de índice dos. No obstante, las raíces cúbicas también son bastante típicas, que son aquellas que tienen índice tres. A partir del índice cuatro no son tan comunes, pero no es difícil comprenderlas.

Raíces cuadradas típicas:

• √1 = ± 1
• √4 = ± 2
• √9 = ± 3
• √16 = ± 4
• √25 = ± 5
• √36 = ± 6
• √49 = ± 7
• √64 = ± 8
• √81 = ± 9
• √100 = ± 10
• ...

Raíces cúbicas típicas:

• ∛1 = 1
• ∛-1 = -1
• ∛8 = 2
• ∛-8 = -2
• ∛27 = 3
• ∛-27 = -3
• ...

En la práctica, las raíces cuadradas se utilizan en una variedad de aplicaciones, desde cálculos de áreas hasta estimaciones estadísticas. Las raíces cúbicas, por otro lado, son especialmente útiles en cálculos de volumen y en ciertas áreas de la ingeniería.

Por ejemplo, calcular la raíz cúbica de un número puede ser esencial para entender cómo se distribuye un volumen en un espacio tridimensional. En este sentido, la radicación se convierte en una herramienta versátil que ayuda a abordar problemas complejos de manera más sencilla y efectiva.

Vamos a ver qué tal estás entendiendo la lección haciendo los siguientes ejercicios, para que puedas practicar:

1. Establece si las siguientes oraciones son verdaderas o falsas:

• Las raíces con índice par tienen un doble resultado (positivo y negativo).
• Las raíces con índice par no pueden hacerse sobre un número negativo.
• Las raíces con índice impar no pueden hacerse sobre un número negativo.

2. Calcula paso a paso estas raíces:

• √81
• √576
• ∛216
• ∛-2744

Estos ejercicios están diseñados para consolidar la comprensión de las propiedades y aplicaciones de la radicación. Practicar regularmente con diferentes tipos de raíces puede aumentar tu habilidad para resolver problemas matemáticos de manera eficiente.

Imagen: Youtube

1.

• Las raíces con índice par tienen un doble resultado (positivo y negativo).
• Las raíces con índice par no pueden hacerse sobre un número negativo.
• Las raíces con índice impar no pueden hacerse sobre un número negativo.

2.

• √81 => 9 * 9 = 81, pero también (-9) * (-9) = 81, así que las respuestas son 9 y -9.
• √576 => 24 * 24 = 576, pero también (-24) * (-24) = 576, así que las respuestas son 24 y -24.
• ∛216 => 6 * 6 * 6 = 216, así que la respuesta es 6.
• ∛-2744 => (-14) * (-14) * (-14) = -2744, así que la respuesta es -14.

Con estos resultados, puedes verificar tu comprensión de las propiedades de la radicación. Estas soluciones también ilustran cómo las raíces cuadradas ofrecen soluciones múltiples y cómo las raíces cúbicas pueden aplicarse a números negativos, proporcionando una visión más completa de esta operación matemática.

Si deseas leer más artículos parecidos a Qué es la radicación y sus propiedades - con ejemplos, te recomendamos que entres en nuestra categoría de Operaciones básicas.