Qué es la hipotenusa y su fórmula


La hipotenusa es el lado opuesto al ángulo recto de un triángulo rectángulo. En una nueva lección de unProfesor estudiaremos qué es la hipotenusa y su fórmula. Comenzaremos con la definición y fórmula de la hipotenusa, luego veremos algunos ejemplos de su aplicación. Seguiremos con el teorema de Pitágoras y recordaremos cuáles son los triángulos rectángulos. Para finalizar realizaremos ejercicios con el teorema.
Qué es la hipotenusa
La hipotenusa es el lado opuesto al ángulo recto de un triángulo rectángulo. Siempre que utilicemos la fórmula para calcularla debemos estar seguros de utilizar estos triángulos, ya que para triángulos que no tienen un ángulo recto no se puede usar.
La hipotenusa de un triángulo rectángulo es el lado que posee más longitud.

Fórmula de la hipotenusa - con ejemplos
La fórmula de la hipotenusa es la siguiente:
h = raíz (a2 + b2)
Sabiendo que h es la hipotenusa, mientras que a y b son los lados restantes llamados catetos.
Cada vez que debamos resolver el cálculo de la hipotenusa, podremos directamente utilizar esta fórmula para hallar la respuesta.
Ejemplos
1) Averigua el valor de la hipotenusa de un triángulo rectángulo cuyos catetos miden a = 16 cm y b = 20 cm
Utilizamos la fórmula de la hipotenusa, cambiando las incógnitas por los valores que tenemos:
- h = raiz(162 + 202)Resolvemos las potencias
- h = raiz(256 + 400)Realizamos la suma
- h = raiz(656)Resolvemos la raíz cuadrada
- h = 25.6
- El valor de la hipotenusa es h = 25.6 cm.
2) Averigua el valor de la hipotenusa de un triángulo rectángulo cuyos catetos miden a = 10 cm y b = 8 cm
Utilizamos la fórmula de la hipotenusa, cambiando las incógnitas por los valores que tenemos:
- h = raiz(102 + 82)Resolvemos las potencias
- h = raiz(100 + 64)Realizamos la suma
- h = raiz(164)Resolvemos la raíz cuadrada
- h = 12.8
El valor de la hipotenusa es h = 12.8 cm.
Esta fórmula se desprende directamente del teorema de Pitágoras.

Teorema de Pitágoras para entender la fórmula de la hipotenusa
El teorema de Pitágoras fue realizado por un matemático llamado “Pitágoras” quien descubrió que los triángulos rectángulos tenían una propiedad interesante. Esta propiedad es que el cuadrado de la medida de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Este teorema sólo puede utilizarse con triángulos rectángulos, ya que con aquellos triángulos que no poseen un ángulo recto, esta igualdad no se cumple.
El teorema de Pitágoras utiliza tres elementos que componen a los triángulos rectángulos, y ellos son:
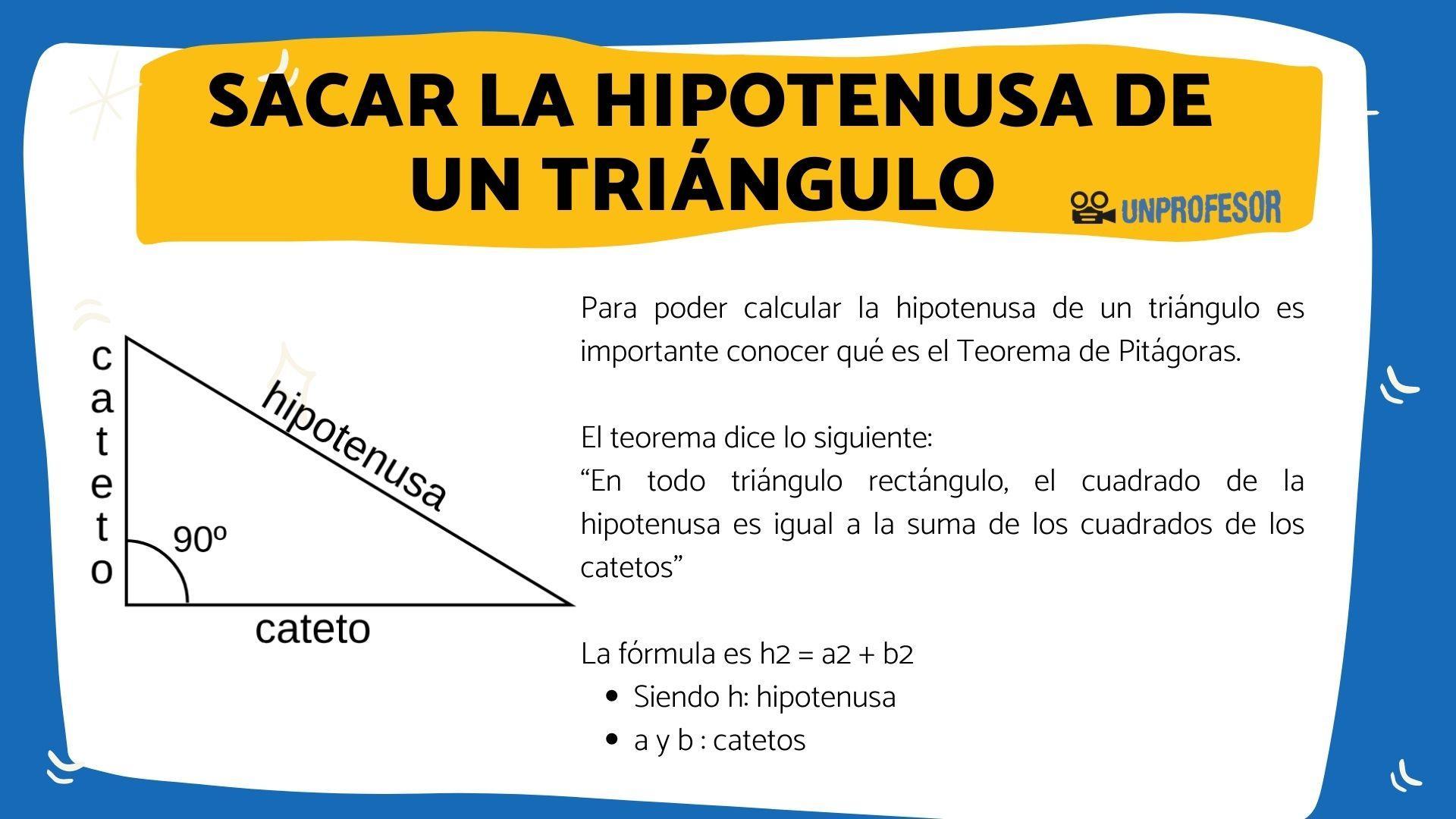
- Hipotenusa: la hipotenusa es el lado más largo que tiene el triángulo rectángulo. También podemos encontrarlo como el lado opuesto al ángulo recto. Según el teorema la longitud de este lado al cuadrado, será igual a la suma de los cuadrados de los otros dos lados restantes.
- Catetos: los catetos son los dos lados que se encuentran formando el ángulo recto. Sus longitudes son más pequeñas que la hipotenusa, ya que según el teorema la suma de los cuadrados de las longitudes de los catetos será igual al cuadrado de la hipotenusa.
La fórmula del teorema de Pitágoras
La fórmula que se utiliza para calcular el teorema de Pitágoras es:
h2 = a2 + b2
Sabiendo que:
- h: hipotenusa
- a y b : catetos
El Teorema de Pitágoras es muy útil cuando se deben realizar cálculos por ejemplo de distancias entre dos puntos que forman un ángulo recto, es decir, si queremos construir una escalera podemos calcular su longitud con la medida de los catetos, donde uno sería la longitud del piso y el otro la altura que queremos darle a la misma. Además si quiero calcular la distancia entre un punto y el otro que forman un ángulo recto, puedo calcular la hipotenusa que los une con el teorema.
Es una de las fórmulas matemáticas más importantes y utilizadas porque tiene muchísimas aplicaciones y muy diversas en cuanto al cálculo de distancias, áreas, alturas, etc. En trigonometría se utiliza para el cálculo del seno, coseno y tangente de los triángulos rectángulos.
Qué son los triángulos rectángulos
Recordemos que un triángulo rectángulo es aquel triángulo que posee uno de sus ángulos rectos, mientras que los otros dos serán agudos y complementarios. Debido a que la suma de los ángulos interiores de un triángulo es igual a 180° sexagesimales y sabiendo que uno de ellos mide 90° sexagesimales, entonces la suma de los dos ángulos restantes será igual a 90° sexagesimales.

Ejemplos del teorema de Pitágoras
Aquí vamos a dejarte con ejemplos del teorema de Pitágoras para que te quede clara la lección:
1) Averigua el valor de la hipotenusa sabiendo que los catetos de un triángulo rectángulo son a= 4 cm y b= 3 cm
Recordemos que el teorema de Pitágoras tiene su fórmula
h2 = a2 + b2
Entonces aplicamos el mismo cambiando las incógnitas por los valores que nos dice el problema a resolver.
- h2 = 42 + 32
- h2 = 16 + 9Resolvemos los cuadrados
- h2 = 25Realizamos la suma
- h = raiz(25)Realizamos la operación opuesta a la potencia para despejar h
- h = 5
Por lo tanto la hipotenusa de un triángulo rectángulo cuyos catetos miden 4 cm y 3 cm es igual a 5 cm. Como sabemos la hipotenusa es el lado más largo del triángulo, por lo tanto según el resultado tiene coherencia que mida 5 cm.
2) Averiguar el valor del cateto sabiendo que el triángulo rectángulo tiene una hipotenusa de medida h=9 cm y un cateto a=5 cm.
Aplicamos el teorema de Pitágoras cambiando los datos que nos da el ejercicio.
- h2 = a2 + b2
- 92 = 52 + b2
- 81 = 25 + b2 Resolvemos la potencia
- 81 - 25 = b2Realizamos la operación opuesta a la suma
- 56 = b2Resolvemos la resta
- raíz(56) = b Realizamos la operación opuesta a la potencia para despejar b
- 7.48 = b
Entonces el valor del cateto faltante es b = 7.48 cm.
Si deseas leer más artículos parecidos a Qué es la hipotenusa y su fórmula, te recomendamos que entres en nuestra categoría de Trigonometría.