Teorema del seno


El teorema del seno se utiliza en triángulos para conocer la medida de la longitud de un lado o la amplitud de un ángulo interior, ya que establece una relación de proporción entre lados y senos de los ángulos opuestos interiores a ellos. En una nueva lección de unProfesor estudiaremos qué dice el teorema del seno. Comenzaremos con su fórmula, seguiremos con su aplicación para terminar con algunos ejemplos y ejercicios resueltos.
¿Qué dice el teorema del seno?
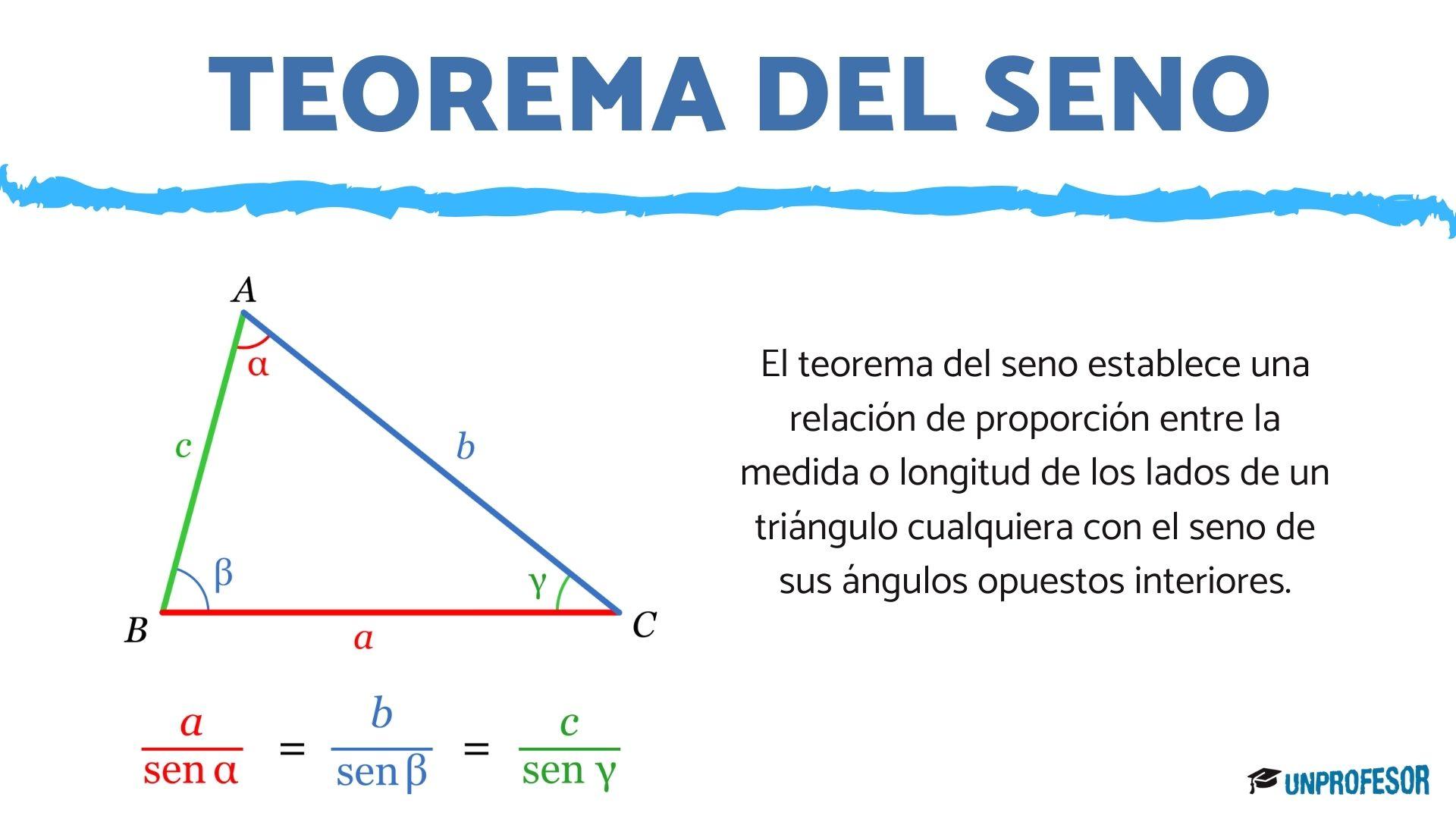
El teorema del seno establece una relación de proporción entre la medida o longitud de los lados de un triángulo cualquiera con el seno de sus ángulos opuestos interiores. Es decir, que existe una relación matemática de proporcionalidad entre la longitud de los lados de un triángulo con los senos de los ángulos interiores que son opuestos a ellos.
Para poder utilizar la fórmula del teorema del seno es necesario conocer el valor de la longitud de dos lados del triángulo y la medida de su ángulo interior opuesto o también la medida de dos ángulos y un lado opuesto a alguno de ellos.
Los ejercicios que se pueden resolver con este teorema, son aquellos donde se quiere conocer la medida de uno de los lados de un triángulo o la amplitud de un ángulo. Como dijimos anteriormente, se deben conocer algunos valores previos para poder resolverlo y obtener un resultado.

Teorema del seno: fórmula
La longitud de los lados de un triángulo cualquiera son proporcionales al seno de sus ángulos opuestos.
Con esto queremos decir que, cada lado establece una relación de proporcionalidad con el seno del ángulo opuesto.
Veamos la fórmula del Teorema del seno:
Tenemos un triángulo cualquiera cuyos ángulos interiores son A, B y C. Los lados del mismo los vamos a nombrar teniendo en cuenta que cada lado opuesto a un ángulo llevará el mismo nombre pero con una letra minúscula, entonces el lado opuesto al ángulo A se llamará a, el opuesto a B se llamará b mientras que el lado opuesto a C se llamará c.
Entonces la fórmula del teorema del seno será:
a / senA = b / senB = c / senC
Si bien el teorema del seno establece la relación entre los tres lados y los tres ángulos, para resolver los ejercicios se utiliza una igualdad entre dos razones, por lo que necesitamos conocer tres valores para averiguar el resultado del cuarto valor faltante.

¿Cómo se aplica el teorema del seno?
Averiguar el valor del ángulo B de un triángulo cuyas medidas son a = 6 cm, b = 8 cm y el ángulo A = 45°.
Primero planteamos el teorema del seno con los lados a y b, y los ángulos A y B:
a / senA = b / senB
Reemplazamos los valores conocidos:
6 / sen45 = 8 / senB
Aplicamos el producto cruzado de proporcionalidad:
6 . senB = 8 . sen45
Despejamos ahora como una ecuación:
senB = (8 . sen45) / 6
Y luego aplicamos la operación inversa del seno de un ángulo para despejar B y obtener el resultado:
B = arcsen (8 . sen45) / 6
B = 70°
Entonces la medida del ángulo interior B que obtuvimos es igual a 70°.

Teorema del seno: ejemplos
Otro ejemplo que podemos visualizar a la hora de utilizar el teorema del seno, es cuando tenemos la medida de dos ángulos interiores de un triángulo y uno de sus lados opuestos, y queremos averiguar el valor del lado faltante.
Tenemos un triángulo cualquiera, y sabemos que A = 40° y C = 95°. El lado a tiene una longitud de 20 cm y queremos averiguar la medida del lado c.
Para ellos utilizamos la fórmula del teorema del seno:
a / senA = c / senC
Reemplazamos con los valores que conocemos:
20 / sen40 = c / sen95
Aplicamos el producto cruzado por la proporcionalidad:
20 . sen95 = c . sen40
Despejamos c de la ecuación:
(20 . sen95) / sen40 = c
30.99 = c
Entonces la longitud del lado c = 30.99 cm.
Si queremos conocer el valor del ángulo B, sabiendo que su lado b, mide 22 cm podemos resolverlo con los valores de A y a que sabíamos según el ejercicio o el valor de C conocido y c obtenido. Siempre es recomendable utilizar los valores otorgados por el ejercicio para evitar posibles errores.
Utilizamos nuevamente la fórmula del seno:
a / senA = b / senB
Reemplazamos por los valores que conocemos:
20 / sen40 = 22 / senB
Aplicamos producto cruzado:
20 . senB = 22 . sen40
Despejamos la ecuación:
senB = (22 . sen40) / 20
Aplicamos la operación inversa al seno:
B = arcsen ((22 . sen40) / 20)
B = 45°
El valor del ángulo B = 45°
Teorema del seno: problemas resueltos
Te dejamos problemas resueltos del Teorema del Seno para que puedas practicar en casa.
Problema 1
Un triángulo cualquiera tiene medida de sus lados a=15 cm y c= 17 cm, y sabemos que el ángulo C = 60°. ¿Cuánto mide la amplitud de A?
Aplicamos el teorema del seno
a / senA = c / senC
Reemplazamos por los valores que conocemos
15 / senA = 17 / sen60
Aplicamos producto cruzado
15 . sen60 = 17 . senA
Despejamos de la ecuación
(15 . sen60) / 17 = senA
Aplicamos la operación inversa del seno
arcsen((15 . sen60) / 17) = A
49.8° = A
La amplitud de A mide 49.8°.
Problema 2
Tenemos un triángulo cuyas medidas de ángulos interiores son B=30° y C=80° y lado b=12 cm. ¿Cuál es la longitud del lado c?
Aplicamos el teorema del seno
b / senB = c / senC
Reemplazamos por los valores que conocemos
12 / sen30 = c / sen80
Aplicamos producto cruzado
12 . sen80 = c . sen30
Despejamos de la ecuación
(12 . sen80) / sen30 = c
23.63 = c
La longitud de c es 23.63 cm.
Ahora bien, conocemos también el lado a que mide 22.55 cm y queremos averiguar la apertura de A.
Aplicamos el teorema del seno
a / senA = b / senB
Reemplazamos por los valores que conocemos
22.55 / senA = 12 / sen30
Aplicamos producto cruzado
22.55 . sen30 = 12 . senA
Despejamos de la ecuación
(22.55 . sen30) / 12 = senA
Aplicamos la operación inversa del seno
arcsen((22.55 . sen30) / 12) = A
70° = A
La amplitud de A mide 70°.
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.
Si deseas leer más artículos parecidos a Teorema del seno, te recomendamos que entres en nuestra categoría de Trigonometría.