Qué es la trigonometría


En unProfesor os explicaremos qué es la trigonometría. Con esto vamos a ver unas pautas generales y luego lo aplicaremos a casos concretos que vamos a estudiar.
La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. Deriva de los términos griegos 'triángulo' y 'medida'.
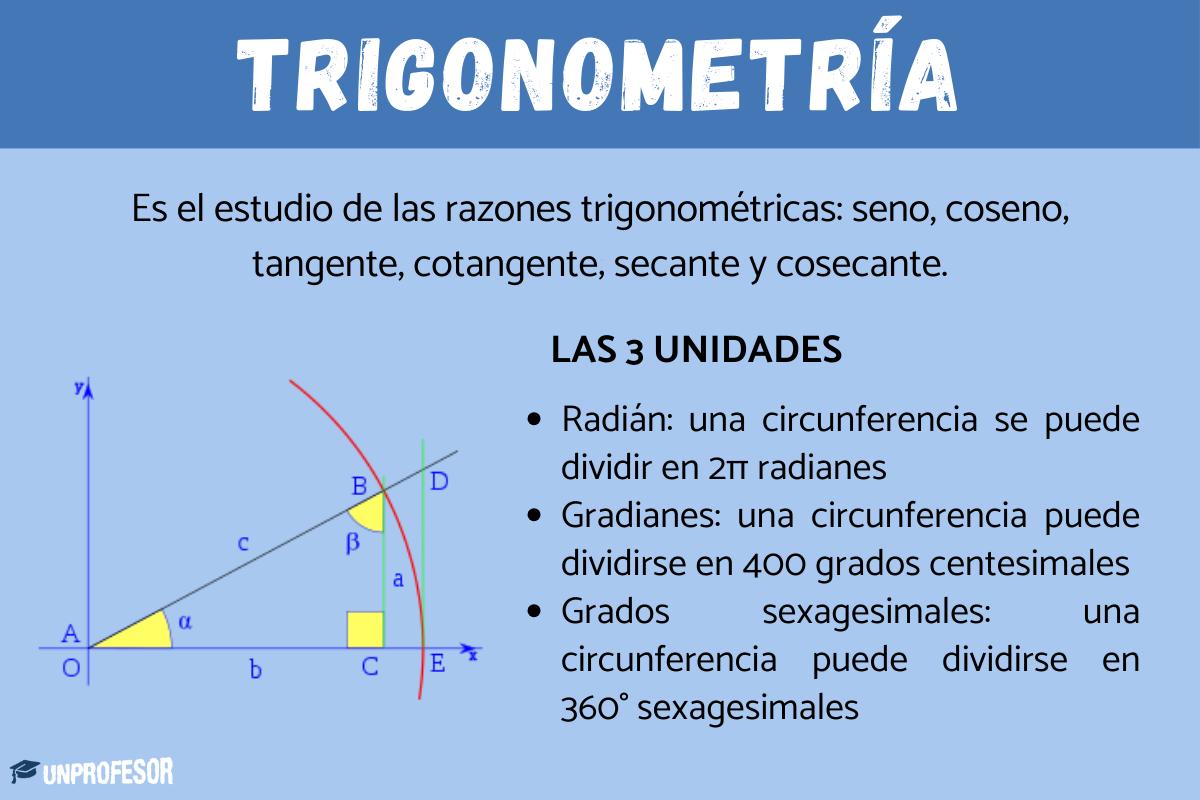
En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión.
Los triángulos son polígonos con tres lados y tres ángulos. La suma de sus tres ángulos suma 180º. Expresamos los ángulos: A, B y C. Expresamos los lados: a,b y c. En el vídeo podrás ver gráficamente cómo colocar y nombrar los lados y ángulos de un triángulo.
Qué es la trigonometría - definición para niños
Cuando hablamos de trigonometría nos estamos refiriendo a la medición de triángulos. Esta rama de la matemática es la encargada de estudiar las razones trigonométricas de los triángulos tales como el coseno, seno, tangente, cotangente, cosecante y secante. Esto quiere decir, que estudia la relación que existe entre los lados y ángulos de los triángulos.
En aquellas cuestiones de la geometría en donde se necesita medir con precisión es cuando la trigonometría se utiliza.
Unidades de la trigonometría
La trigonometría utiliza tres unidades de medida para calcular la amplitud de los ángulos en cuestión. Las tres unidades son:
- Radián: una circunferencia se puede dividir en 2π radianes
- Gradianes: una circunferencia puede dividirse en 400 grados centesimales
- Grados sexagesimales: una circunferencia puede dividirse en 360° sexagesimales

¿Para qué sirve la trigonometría?
La trigonometría se utiliza en muchos cálculos de la vida diaria que necesitan mediciones precisas y exactas, tales como astronomía, física, náutica, telecomunicaciones, cartografía, ingeniería, navegación satelital, etc.
Su uso más frecuente es para medir distancias grandes sin la necesidad de recorrer los trayectos, como por ejemplo el de las estrellas. También se utiliza para la medición de ángulos de inclinación y alturas en lugares que no son accesibles.

Funciones trigonométricas - ejemplo
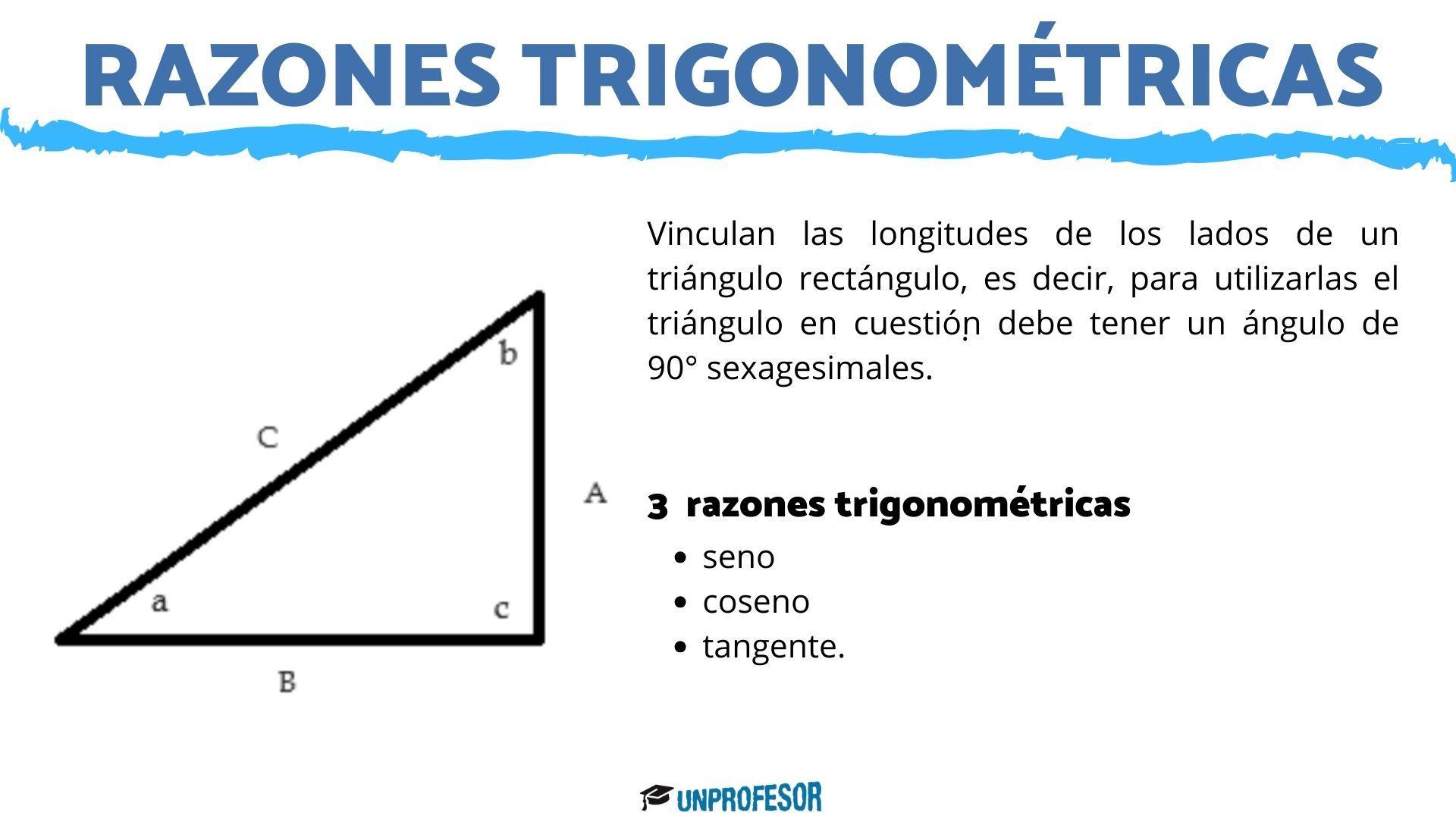
Como bien dijimos anteriormente, las funciones trigonométricas son las que establecen una relación entre ángulos y lados de un triángulo rectángulo. Todo triángulo rectángulo posee uno de sus ángulos rectos, de 90° sexagesimales, y a partir de esto se establecen cuáles son los catetos y cuál es la hipotenusa.
- Catetos: los catetos son dos lados, aquellos que forman al ángulo recto. Cuando realizamos alguna de las razones trigonométricas para estudiar uno de los ángulos restantes, podemos decir que un cateto será opuesto a este, mientras que el otro será adyacente.
- Hipotenusa: la hipotenusa es el lado que se encuentra opuesto al ángulo de 90° sexagesimales, y es que tiene mayor medida de los tres.
Ejemplo
Pensemos en un triángulo rectángulo cuyos catetos sean A y B, la hipotenusa H, y el ángulo a estudiar x.
A partir de esto, surgen las razones trigonométricas básicas que son:
- Seno: el seno de un ángulo es igual a la razón entre el cateto opuesto y la hipotenusa.
- sen x = cat. opuesto / hipotenusa = A / H
- Coseno: el coseno de un ángulo es igual a la razón entre el cateto adyacente y la hipotenusa.
- cos x = cat. adyacente / hipotenusa = B / H
- Tangente: la tangente de un ángulo es igual a la razón entre el cateto opuesto y el cateto adyacente.
- tg x = cat. opuesto / cat. adyacente = A / B
De estas razones trigonométricas se desprenden sus razones recíprocas que son:
- Cosecante: la cosecante de un ángulo es igual a la razón entre la hipotenusa y el cateto opuesto.
- cosec x = hipotenusa / cat. opuesto = H / A
- Secante: la secante de un ángulo es igual a la razón entre la hipotenusa y el cateto adyacente.
- cosec x = hipotenusa / cat. adyacente = H / B
- Cotangente: la cotangente de un ángulo es igual a la razón entre el cateto adyacente y el cateto opuesto.
- cotg x = cat. adyacente / cat. opuesto = B / A
Aquí te contamos cuáles son las razones trigonométricas.

¿Cómo se utiliza la trigonometría?
Conociendo ya cuáles son las razones trigonométricas, podemos utilizarlas para averiguar el valor de un ángulo o un lado faltante en un triángulo rectángulo. Para poder hacerlo necesitamos:
- Primero: determinar cuáles son los valores conocidos, tanto lados como ángulos, y por lo tanto señalar cuales son los valores faltantes.
- Segundo: Elegir la razón trigonométrica que habrá que utilizar teniendo en cuenta los valores conocidos y el valor que hay que hallar.
- Tercero: Reemplazar los datos en la ecuación planteada según la razón elegida.
- Cuarto: Revolver la ecuación y descubrir la incógnita.

Trigonometría: ejercicio resuelto
Aquí tienes un ejercicio de trigonometría con solución para que practiques en casa.
Ejercicio
Un triángulo rectángulo con medida de un catetos A = 5 cm. Uno de sus ángulos mide x = 45°. Hallar el ángulo faltante, el otro cateto y la hipotenusa.
Solución
Conocemos la medida de un cateto y dos de sus ángulos, ya que uno mide 45° sexagesimales según nos indica el ejercicio, y el otro mide 90° sexagesimales por ser recto.
Comencemos con la medida de la hipotenusa, para ello podemos utilizar el seno ya que en este caso, el cateto conocido es el opuesto al ángulo de 45°.
- sen x = cat. opuesto / hipotenusa = A / H
- sen 45° = 5 / H
- H = 5 / sen 45°
- H = 7,07 cm
Ahora que conocemos la hipotenusa y uno de los catetos podemos utilizar el coseno para hallar el cateto adyacente.
- cos x = cat. adyacente / hipotenusa = B / H
- cos 45° = B / 7,07
- cos 45° . 7,07 = B
- 5 cm = B
Para hallar el ángulo restante, podemos utilizar ahora cualquiera de las tres razones trigonométricas. Vamos a utilizar la tangente, debido a que aún no la hemos usado.
- tg y = cat. opuesto / cat. adyacente = B / A
- tg y = 5 / 5
- y = arctg (5 / 5)
- y = 45°
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.
Si deseas leer más artículos parecidos a Qué es la trigonometría, te recomendamos que entres en nuestra categoría de Trigonometría.