Cómo resolver ecuaciones con dos incógnitas

Para resolver ecuaciones con dos incógnitas, primero debemos recordar el concepto de ecuaciones. Las ecuaciones son igualdades algebraicas que tienen en su composición un elemento desconocido llamado incógnita que se denota con una letra. Se resuelve la misma de forma tal, que se nos permita conocer el valor faltante que cumpla con la igualdad.

Las ecuaciones tienen grados que definen qué tipo de ecuación será, y se sabe a partir del exponente de mayor valor que tiene la incógnita. Dos o más ecuaciones son equivalentes si tienen el mismo resultado para el valor desconocido, es decir si la solución es la misma.

Ahora bien, si queremos resolver ecuaciones con dos incógnitas es muy importante saber que se necesitan al menos dos ecuaciones para poder resolverlas.

Esto se debe a que con una sola igualdad es imposible resolver el valor de dos incógnitas, debido a que si despejamos el valor de una de ellas, quedará su ecuación con respecto a la otra y allí nos encontramos con un inconveniente sin resolución. A estas dos ecuaciones que responden a una misma respuesta, se les llama sistema de ecuaciones. Las ecuaciones que generalmente se utilizan son de grado lineal, es decir que las incógnitas tienen sus exponentes iguales a 1.

Un sistema de ecuaciones, por ejemplo, se ve de la siguiente manera:

• 2x + y = 6
• 4x + 3y = 14

Al resolver el sistema de ecuaciones, podemos hallar que el mismo tiene una solución, ninguna solución o infinitas soluciones.

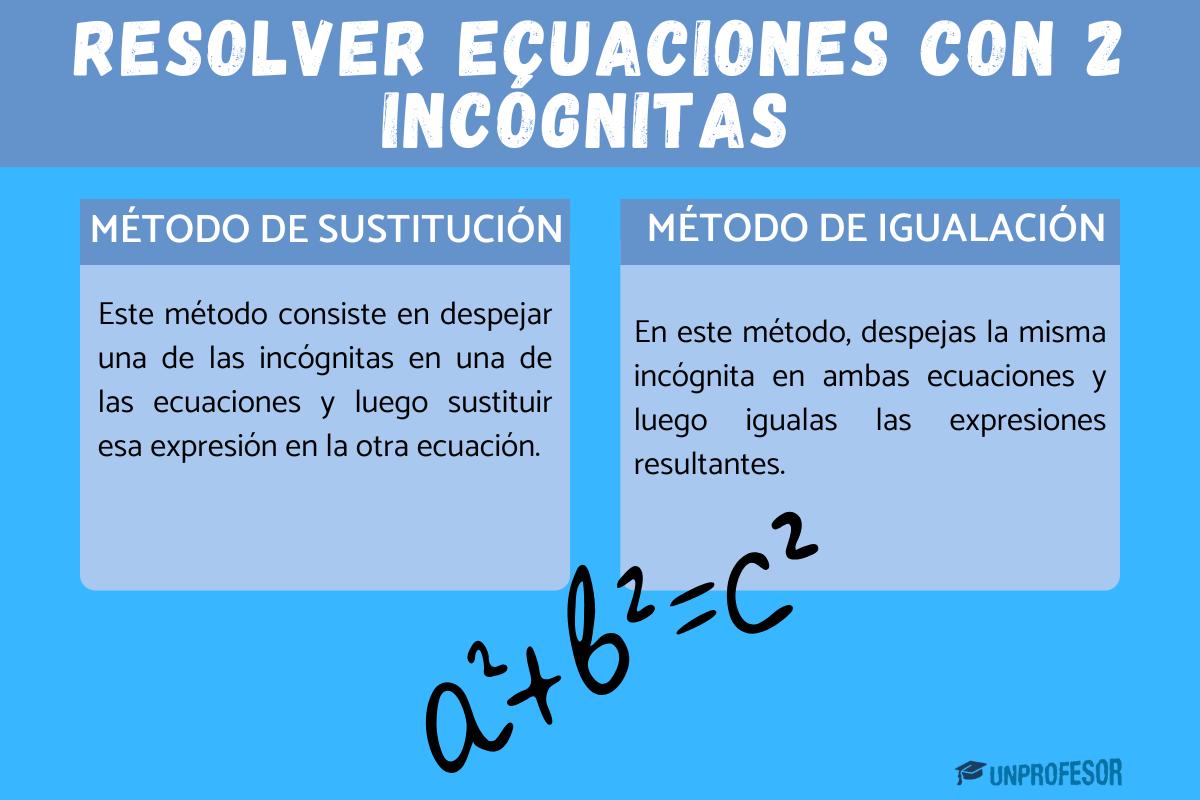
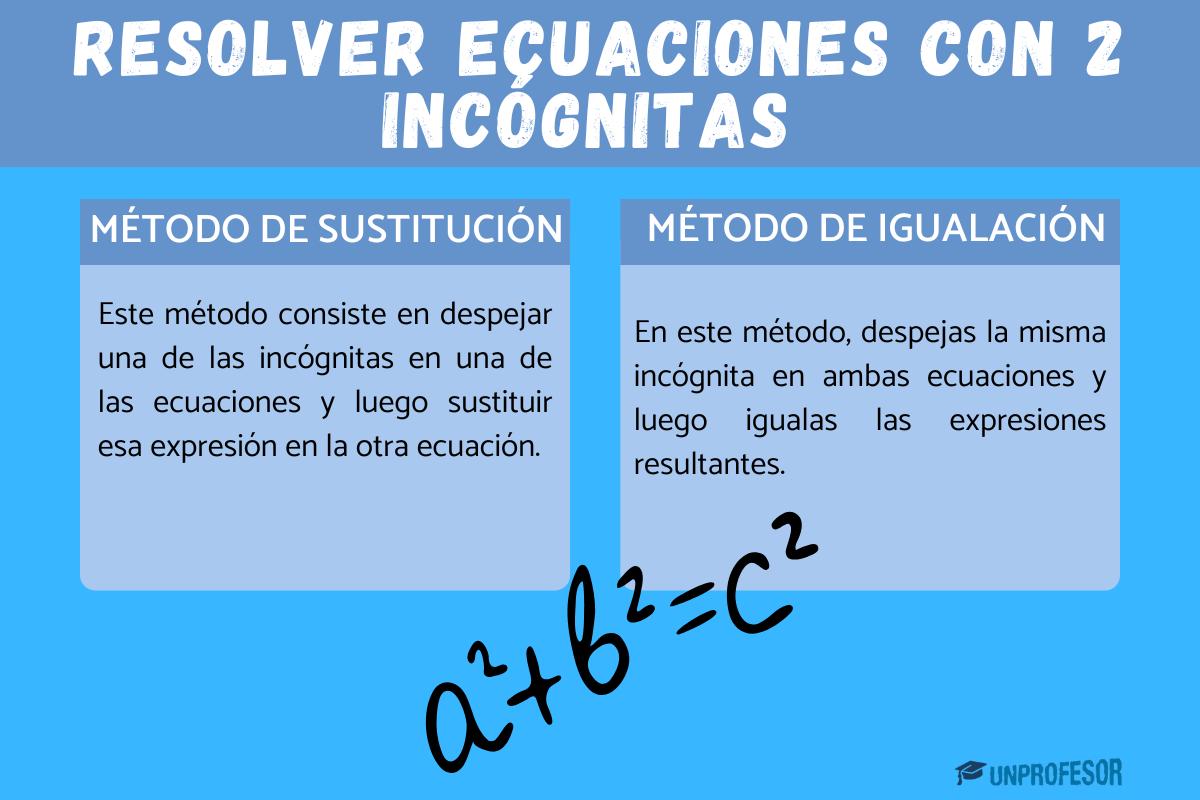
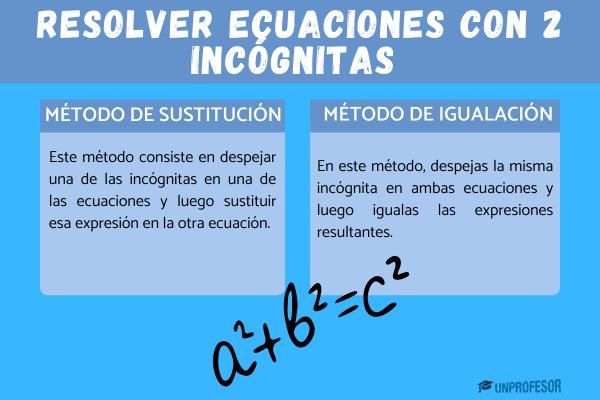
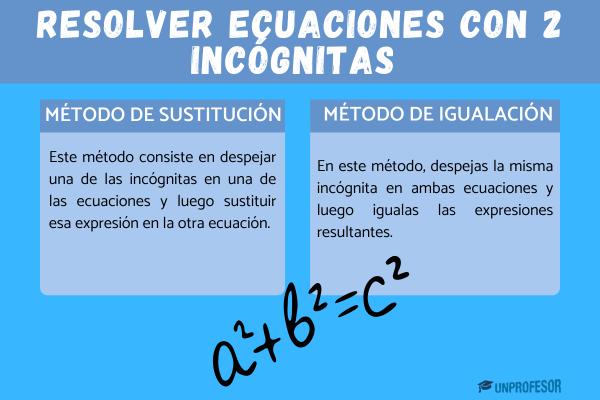
Existen varios métodos para resolver un sistema de ecuaciones, entre ellos los más utilizados son el método de igualación, y el método de sustitución.

Te dejamos un vídeo de nuestro profesor donde te cuenta qué es un sistema de ecuaciones:

Como mencionamos anteriormente, existen varios métodos de resolución, pero en este apartado veremos los dos más utilizados.

Método de igualación

Para realizar el método de igualación debemos despejar la misma incógnita en las dos ecuaciones para luego igualarlas. Es decir, de las dos ecuaciones, elegimos una de las incógnitas y la despejamos en ambas, para luego igualarlas y así convertir un sistema de dos ecuaciones de dos incógnitas en una ecuación de una sola incógnita. Una vez hallado el valor de esta, reemplazamos en las dos ecuaciones para hallar el valor faltante y así determinar la solución.

Veamos cómo se resuelve utilizando el ejemplo anterior.

• 2x + y = 6
• 4x + 3y = 14

Primero, elegimos la incógnita que queremos despejar. Como en la primera ecuación la y tiene coeficiente uno, entonces será más sencillo despejarla.

• y = 6 - 2x
• y = (14 - 4x) / 3

Ahora como el resultado de y debe ser el mismo en ambas ecuaciones, sabemos que son iguales y entonces igualamos, tal como el método lo anticipa, las dos ecuaciones:

• y = y
• 6 - 2x = (14 - 4x) / 3

Tenemos ahora, una ecuación lineal de una sola incógnita, y resolvemos para hallar el valor de x.

• (6 - 2x) . 3 = 14 - 4x
• 18 - 6x = 14 - 4x
• 18 - 14 = -4x + 6x
• 4 = 2x
• 4 / 2 = x
• 2 = x

El resultado de x es igual a 2. Con este dato, en las ecuaciones que despejamos reemplazamos el valor de x, y debemos hallar el mismo resultado de y para ambas.

• y = 6 - 2x = 6 - 2 . 2 = 6 - 4 = 2
• y = (14 - 4x) / 3 = (14 - 4 . 2) / 3 = (14 - 8) / 3 = 6 / 3 = 2

Entonces el resultado del sistema de ecuaciones, se escribe como un punto en un sistema de coordenadas cartesianas, y es: S = (2, 2)

Método de sustitución

Para realizar el método de sustitución, debemos elegir una de las incógnitas que forman parte de nuestro sistema de ecuaciones lineales, y despejarla en una de las ecuaciones, para luego reemplazarla en la ecuación que no utilizamos.

Esto, permite que un sistema con dos incógnitas, se convierta en una ecuación lineal con una sola incógnita para poder hallar el valor de una de ellas primero. Luego, como hicimos con el método anterior, se reemplaza en la ecuación que despejamos y encontramos el valor de la segunda incógnita.

Veamos cómo se resuelve utilizando el ejemplo anterior.

• 2x + y = 6
• 4x + 3y = 14

Primero, elegimos la incógnita que queremos despejar, utilizando la misma lógica que en el método de igualación. Como la y tiene coeficiente uno en la primera ecuación, despejamos esa misma, y la reemplazamos en la segunda ecuación.

2x + y = 6 —> y = 6 - 2x

Ahora reemplazamos y en la ecuación que aún no utilizamos:

• 4x + 3y = 14
• 4x + 3(6 - 2x) = 14
• 4x + 18 - 6x = 14
• 4x - 6x = 14 - 18
• -2x = -4
• x = -4 / -2
• x = 2

Ya sabemos que x vale 2, entonces reemplazamos en la ecuación que habíamos despejado para hallar el valor de y.

y = 6 - 2x = 6 - 2 . 2 = 6 - 4 = 2

Entonces el resultado del sistema de ecuaciones, se escribe como un punto en un sistema de coordenadas cartesianas, y es: S = (2, 2)

Un sistema de ecuaciones lineales con dos incógnitas puede tener diferentes soluciones finales y se clasifican de la siguiente manera:

• Compatible determinado: es una sistema de ecuaciones lineales que posee una única solución, es decir un sólo valor posible para cada una de las incógnitas. Cuando se representa en el eje cartesiano, son las ecuaciones de dos rectas que se cortan en un único punto.
• Compatible indeterminado: es un sistema de ecuaciones lineales que posee infinitas soluciones, es decir que son infinitos los valores que pueden tomar las dos incógnitas. Cuando se representa en el eje cartesiano, son las ecuaciones de dos rectas coincidentes.
• Incompatible: es una sistema de ecuaciones lineales que no posee solución, es decir que NO existe un valor para cada una de las incógnitas que resuelva el sistema. Cuando se representa en el eje cartesiano, son las ecuaciones de dos rectas paralelas, es decir que no se intersecan en ningún punto nunca.

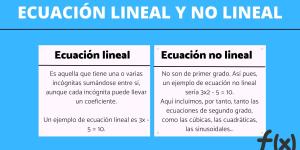
En esta otra lección te damos las diferencias entre ecuaciones lineales y no lineales.

Si deseas leer más artículos parecidos a Cómo resolver ecuaciones con dos incógnitas, te recomendamos que entres en nuestra categoría de Álgebra.