Propiedades de la suma de matrices


En esta lección os explicaremos las propiedades de la suma de matrices. Las matrices son arreglos rectangulares formados por números ubicados en renglones y columnas. Existen propiedades para la suma de estos arreglos. En una nueva lección de unProfesor vamos a estudiar cuáles son las propiedades de las sumas de matrices. Comenzaremos repasando el concepto de matrices, para seguir con la suma y resta. Luego veremos las propiedades de la suma y terminaremos con algunos ejemplos.
En esta lección veréis diferentes ejemplos prácticos de cada propiedad de la suma de matrices. Además, si no lo tenéis bien claro podéis seguir practicando con problemas de este tipo podéis hacer los ejercicios imprimibles con sus soluciones que os he dejado en la web. ¡Suerte en los estudios!
Cuáles son las propiedades de la suma de matrices
La suma de matrices se realiza cuando tienen las mismas dimensiones sumando los números o símbolos en cada una de las posiciones que tienen. Aquí tienes un repaso de las propiedades de la suma de matrices.
Propiedad cerradura
Para sumar matrices se debe tener en cuenta que tengan las mismas dimensiones, es decir si quiero sumar dos matrices, ambas deben tener dimensiones m x n. Veamos un ejemplo. Por ejemplo, si quiero sumar una matriz 3 x 2, entonces deberá ser con otra matriz que también tenga dimensiones 3 x 2.
La suma de dos matrices de m x n, dará como resultado otra matriz m x n. La suma no está definida en dos matrices que NO tienen las mismas dimensiones.
Propiedad conmutativa de la suma
Esta es otra de las propiedades de la suma de matrices. Y es que si tenemos dos matrices de las mismas dimensiones, entonces la propiedad conmutativa de la suma nos indica que podemos sumarlas ordenándolas de cualquier forma y obtendremos el mismo resultado. Es decir, si queremos sumar dos matrices A y B podemos hacerlo sumando A + B o B + A y el resultado será el mismo.
Por ejemplo
- A = 2 3 y B = 3 4
- 4 6 5 7
Entonces A + B = 2 3 + 3 4 = 5 7
- 4 6 5 7 9 13
- Y B + A = 3 4 + 2 3 = 5 7
- 5 7 4 6 9 13
Obtenemos el mismo resultado, una nueva matriz C = 5 7
9 13
Propiedad asociativa de la suma
Si tenemos tres matrices del mismo orden, se puede cambiar la asociación que hay entre ellas y conseguir el mismo resultado, es decir, si tenemos tres matrices A, B y C, entonces podemos hacer (A + B) + C o A + (B + C) y obtendremos el mismo resultado.
Por ejemplo
- A = 1 2 B = 2 4 C = 5 1
- 4 3 6 2 3 2
Entonces aplicamos la propiedad y obtenemos
- (A + B) + C =( 1 2 + 2 4 ) + 5 1 = 3 6 + 5 1 = 8 7
- 4 3 6 2 3 2 10 5 3 2 13 7
- A + (B + C) = 1 2 + ( 2 4 + 5 1 ) = 1 2 + 7 5 = 8 7 4 3 6 2 3 2 4 3 9 4 13 7
Obtenemos el mismo resultado en ambos casos.
Propiedad de la identidad
La propiedad identidad es otra de las propiedades de la suma de matrices y se utiliza cuando sumamos una matriz cualquiera con una matriz cero de las mismas dimensiones. Una matriz cero está compuesta por ceros en todos sus lugares, es decir que no contiene ningún otro número o letra que no sea cero.
El resultado de sumar una matriz A con otra matriz cero o también llamada O, dará como resultado la matriz A.
Por ejemplo
- A = 7 9 y O = 0 0
- 20 15 0 0
- A + O = 7 9 + 0 0 = 7 9
- 20 15 0 0 20 15
Obtenemos como resultado la matriz A.
Propiedad del inverso
La suma entre una matriz y su inversa da como resultado la matriz cero. La inversa de una matriz está formada por el opuesto de cada uno de los elementos que forman la matriz inicial. Es decir, la matriz inversa de A será -A, y la suma entre ellas será la matriz O.
Por ejemplo
- A = 5 6 entonces -A = -5 -6
- 9 11 -9 -11
- A + ( - A) = 5 6 + -5 -6 = 0 0
- 9 11 -9 -11 0 0
Obtenemos como resultado la matriz O.
Las propiedades de la suma de matrices son muy parecidas a las propiedades de la suma de números reales. Es decir, las mismas propiedades que utilizamos en la suma de
números reales, se utilizan en la suma de las matrices. Lo único que hay que recordar es que las matrices que utilizamos para la suma deben tener las mismas dimensiones, de lo contrario la suma no está definida.

Qué son las matrices en matemáticas
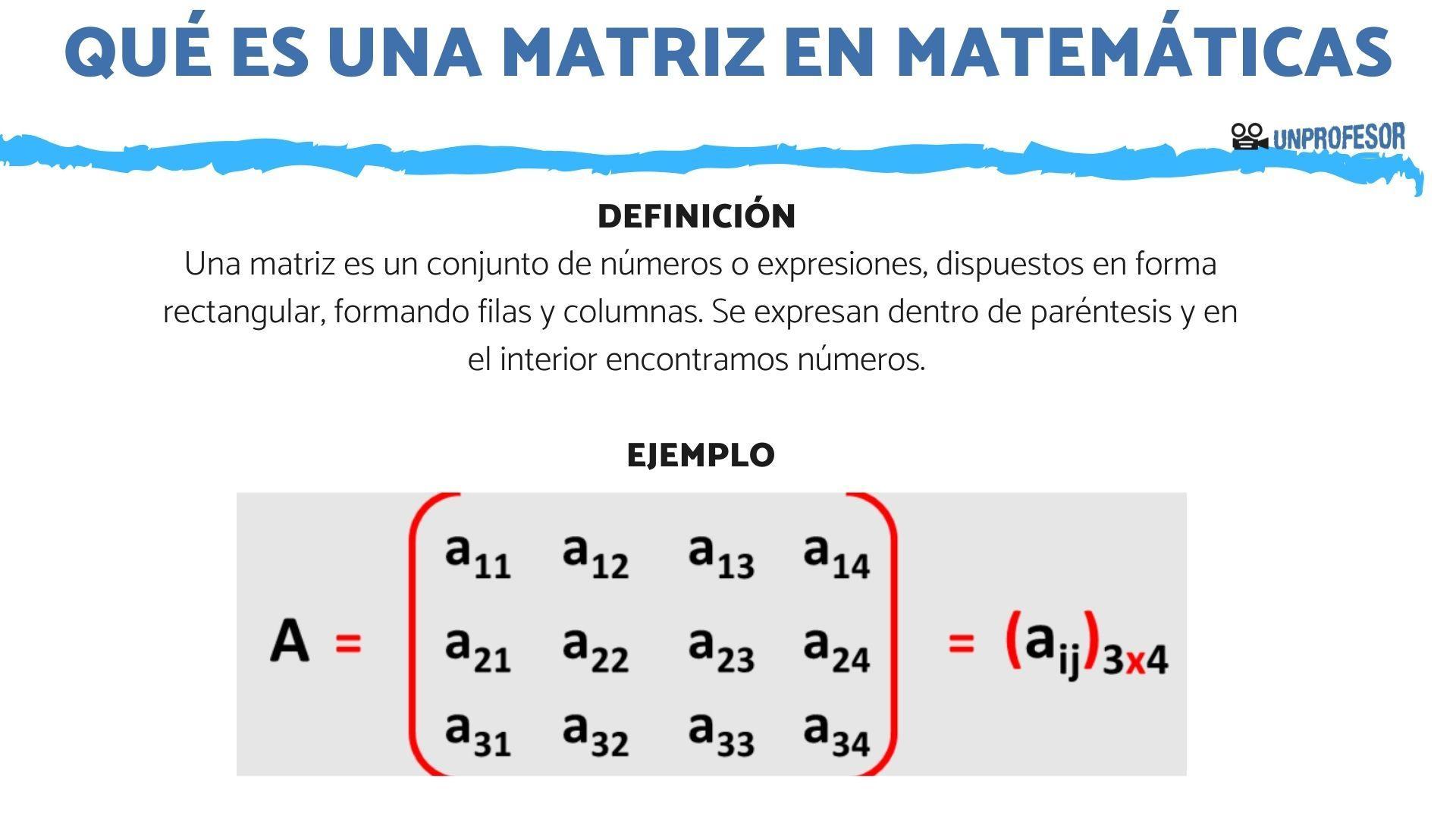
Las matrices son arreglos rectangulares que están formados por números o símbolos ubicados en renglones y columnas. Los elementos de una matriz se ubican en líneas verticales para las columnas y en líneas horizontales para los renglones o filas.
La forma de representar una matriz es con una letra mayúscula con su fila y columna entre paréntesis con letras minúsculas. La dimensión que tiene una matriz indica cuántas filas y columnas posee. Primero se ubican las filas y luego las columnas.
Por ejemplo, si tengo una matriz llamada A con 2 filas y 3 columnas, entonces:
- A ( 2 x 3) = a b c
- d e f
Las matrices pueden sumarse, restarse y multiplicarse.
Aquí te contamos qué es una matriz y ejemplos.

Tipos de matrices
Existen diferentes tipos de matrices y son:
- Matriz rectangular: posee distintos números de renglones y columnas. - Matriz fila: es una matriz rectangular que posee una sola fila.
- Matriz columna: es una matriz rectangular que posee una sola columna - Matriz cero: es una matriz rectangular cuyos componentes son todos iguales a cero. - Matriz cuadrada: es una matriz que posee la misma cantidad de filas que de columnas.
- Matriz diagonal: es una matriz cuadrada que está compuesta por ceros excepto en su diagonal principal, donde posee elementos distintos de cero.
- Matriz escalar: es una matriz diagonal donde los elementos de la diagonal principal son todos iguales.
- Matriz identidad: es una matriz escalar donde los elementos iguales son todos iguales a uno.
- Matriz opuesta: es una matriz donde sus elementos son opuestos al de la matriz original, es decir, tienen el signo contrario.
- Matriz transpuesta: es una matriz donde las filas son columnas y las columnas son filas.

Si deseas leer más artículos parecidos a Propiedades de la suma de matrices, te recomendamos que entres en nuestra categoría de Álgebra.