Suma y resta de matrices


En esta lección de unProfesor vamos a a explicar la suma y resta de matrices. Recordemos que la matriz es un conjunto de números o expresiones, dispuestos en forma rectangular, formando filas y columnas. Para recordar cómo se expresan puedes mirar el vídeo anterior, el concepto de matriz.
La norma para sumar y restar matrices es que el número de filas y de columnas de las matrices que queremos sumar, tiene que ser el número. Si no, no pueden sumarse. Las matrices son conjuntos de números, letras o símbolos que se distribuyen de forma rectangular en columnas y filas, y con ellas se pueden realizar diferentes operaciones matemáticas. En una nueva lección de unProfesor veremos la suma y resta de matrices, cuáles son las propiedades que tienen y algunos ejercicios.
¿Cómo se suman y se restan las matrices? Ejemplos y vídeo
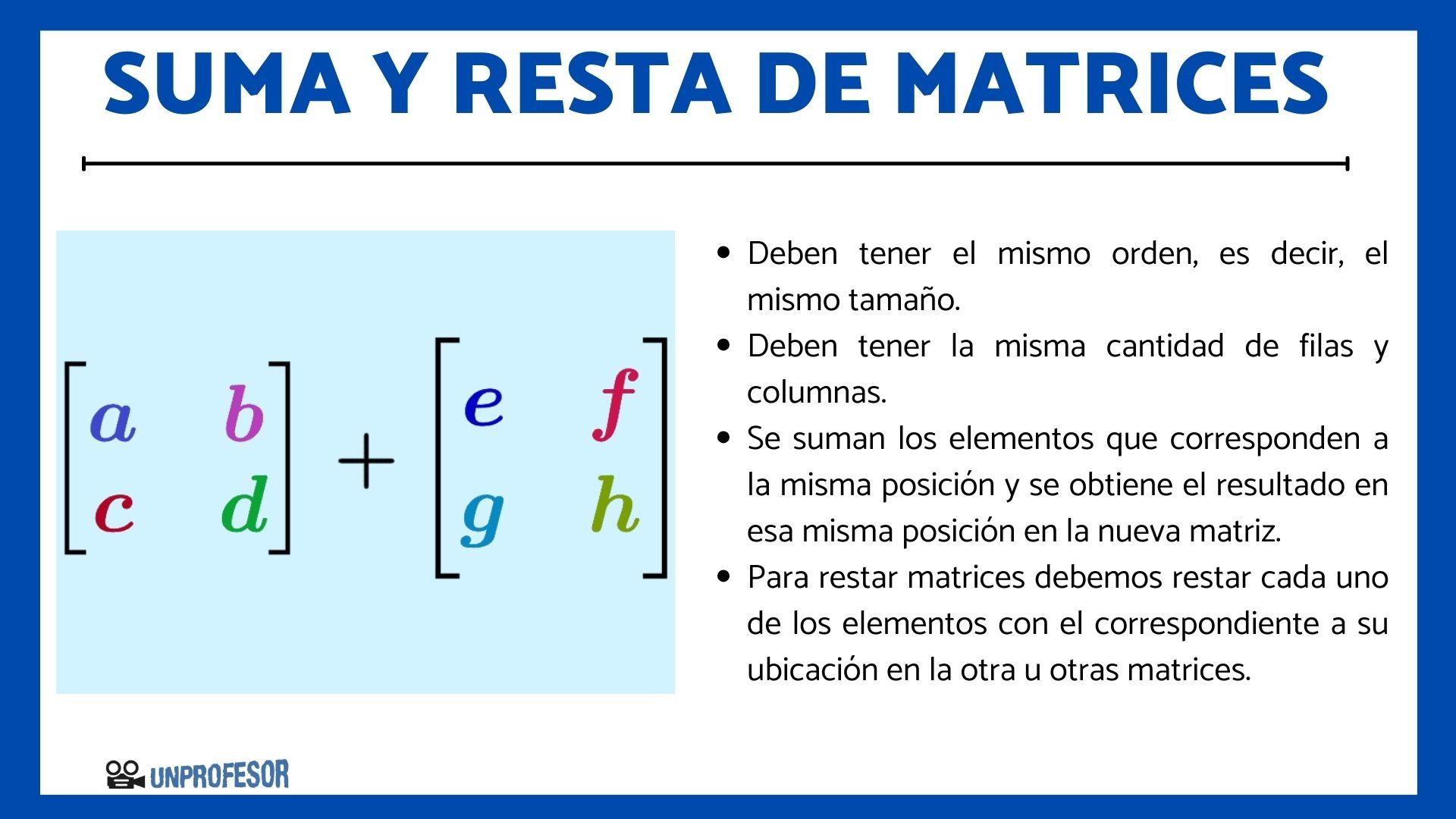
Para sumar o restar matrices, se debe tener en cuenta que estas tengan el mismo orden, es decir, que sean del mismo tamaño. Deberán tener la misma cantidad de filas y columnas para poder realizar las operaciones, de lo contrario no será posible.
Entonces, para sumar dos o más matrices del mismo orden, se suman los elementos que corresponden a la misma posición y se obtiene el resultado en esa misma posición en la nueva matriz, es decir la matriz resultado.
Ejemplo de suma de matrices A + B
- A= 4 2 y B = 3 7
- 6 5 2 3
Las matrices tienen el mismo tamaño, ambas son 2x2, es decir tienen 2 filas y 2 columnas, por lo tanto la suma puede realizarse. Ahora bien, planteamos la suma A + B
- A + B = 4 2 + 3 7 = 4+3 2+7 = 7 9
- 6 5 2 3 6+2 5+3 8 8
- Entonces A + B = 7 9
- 8 8
Ejemplo de resta de matrices C-D
Si por el contrario queremos restar matrices, debemos tener en cuenta que las matrices tienen que ser del mismo orden, tal y como lo hicimos con la suma, y luego restar cada uno de los elementos con el correspondiente a su ubicación en la otra u otras matrices, y el resultado ubicarlo en la nueva matriz en la posición que corresponde.
Veamos un ejemplo: Restamos C - D
- C = 8 9 D = 6 8
- 5 6 2 1
- 7 8 4 2
Las matrices tienen el mismo tamaño, ambas son 3x2, es decir tienen 3 filas y 2 columnas, por lo tanto la resta si puede realizarse. Ahora, planteamos la resta C - D,
- C - D = 8 9 - 6 8 = 8-6 9-8 = 2 1
- 5 6 2 1 5-2 6-1 3 5
- 7 8 4 2 7-4 8-2 3 6
- Entonces C - D = 2 1
- 3 5
- 3 6

Qué es una matriz
Una matriz es un conjunto de números o letras o símbolos que se acomodan en filas y columnas de manera rectangular. Todos sus elementos se organizan de forma vertical y horizontal, y son muy útiles para explicar sistemas de ecuaciones lineales.
Para representar a las matrices se utiliza una letra mayúscula seguido de un número para las filas y luego un número para las columnas. Estos números representan la cantidad de horizontales y verticales que tiene. Por ejemplo, la matriz A de 3 filas y 2 columnas se dice que es una matriz de 3x2.
- A = a b
- c d
- e f

Propiedades de las matrices
La suma y resta de matrices tienen propiedades que se utilizan para poder calcularlas.
Propiedad cerradura
Para sumar o restar matrices debemos tener en cuenta que tengan el mismo tamaño, es decir que dos o más matrices tengan la misma cantidad de filas y columnas para poder realizar las operaciones de suma y resta. Es decir, si queremos sumar o restar dos matrices de orden 2x3, debemos asegurarnos de que ambas sean de orden 2x3, de lo contrario NO es posible realizar estas operaciones.
Propiedad conmutativa de la suma
La propiedad conmutativa únicamente aplica sobre la operación de la suma, ya que si tenemos dos o más matrices del mismo tamaño, podremos aplicar la propiedad y sumar las matrices de cualquier forma, obteniendo así el mismo resultado. No sucede de la misma manera con la resta, en este caso no puede aplicarse esta propiedad, ya que si cambiamos el orden en que restamos las matrices, el resultado no será siempre el mismo. Veamos un ejemplo de ambas operaciones.
Siendo A = 2 5 y B = 5 4
- 6 8 7 1
- Podemos sumar A + B y B + A obteniendo el mismo resultado.
- A + B = 2 5 + 5 4 = 2+5 5+4 = 7 9
- 6 8 7 1 6+7 8+1 13 9
- B + A = 5 4 + 2 5 = 5+2 4+5 = 7 9
- 7 1 6 8 7+6 1+8 13 9
Por lo tanto, no importa el orden en que ubiquemos dos o más matrices con la suma, el resultado siempre será el mismo.
Por el contrario veamos un ejemplo de la resta de dos matrices:
Siendo C = 8 9 y D = 5 7
- 4 5 6 9
- Realizamos las restas C - D y D - C
- C - D = 8 9 - 5 7 = 8-5 9-7 = 3 2
- 4 5 6 9 4-6 5-9 -2 -4
- D - C = 5 7 - 8 9 = 5-8 7-9 = -3 -2
- 6 9 4 5 6-4 9-5 2 4
Por lo tanto, podemos asegurar que no se puede aplicar la propiedad conmutativa de la resta.
Propiedad asociativa de la suma
Si tenemos tres o más matrices que tienen el mismo tamaño, entonces podemos cambiar la asociación que hay entre ellas para la suma, y obtendremos así el mismo resultado. Tal y como lo vimos anteriormente, no aplica para la resta.
Veamos un ejemplo
Siendo A = 2 4 y B = 7 5 y C = 8 1
Las tres matrices son 1x2, tienen una fila y dos columnas, podemos realizar la operación de la suma.
- (A + B) + C = A + (B + C)
- (2 4 + 7 5) + 8 1 = 2 4 + (7 5 + 8 1)
- (2+7 4+5) + 8 1 = 2 4 + (7+8 5+1)
- (9 9) + 8 1 = 2 4 + (15 6)
- 9+8 9+1 = 2+15 4+6
- 17 10 = 17 10
Por lo tanto, el resultado es una nueva matriz 1x2 con los elementos 17 y 10.
Propiedad identidad
La propiedad identidad se utiliza para sumar cualquier matriz junto con una matriz cero del mismo orden. Recordemos que las matrices ceros son aquellas en la que todos sus elementos son ceros. Podemos utilizar esta propiedad en la suma de matrices. Siempre que sumemos la matriz cero a cualquier matriz, obtendremos como resultado esa misma matriz.
Veamos un ejemplo
Siendo A = 5 9 3 y O = 0 0 0
- 4 1 6 0 0 0
- Con dos matrices de orden 2x3 podemos aplicar la propiedad y realizar la operación suma. A + O = 5 9 3 + 0 0 0 = 5+0 9+0 3+0 = 5 9 3 4 1 6 0 0 0 4+0 1+0 6+0 4 1 6
Como resultado obtuvimos la matriz A.
Propiedad del inverso
La propiedad del inverso puede aplicarse a la suma de las matrices que poseen el mismo tamaño. El inverso de una matriz es la misma matriz pero con el signo opuesto en cada uno de sus elementos. Como resultado de esto, se obtiene siempre la matriz cero.
Veamos un ejemplo
- Siendo A = 8 -9 y -A = -8 9
- 5 -1 -5 1
- A + (-A) = 8 -9 + -8 9 = 8 + -8 -9 + 9 = 0 0
- 5 -1 -5 1 5 + -5 -1 + 1 0 0
Como resultado obtenemos la matriz cero.
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Suma y resta de matrices, te recomendamos que entres en nuestra categoría de Álgebra.