Cuáles son las propiedades de las matrices

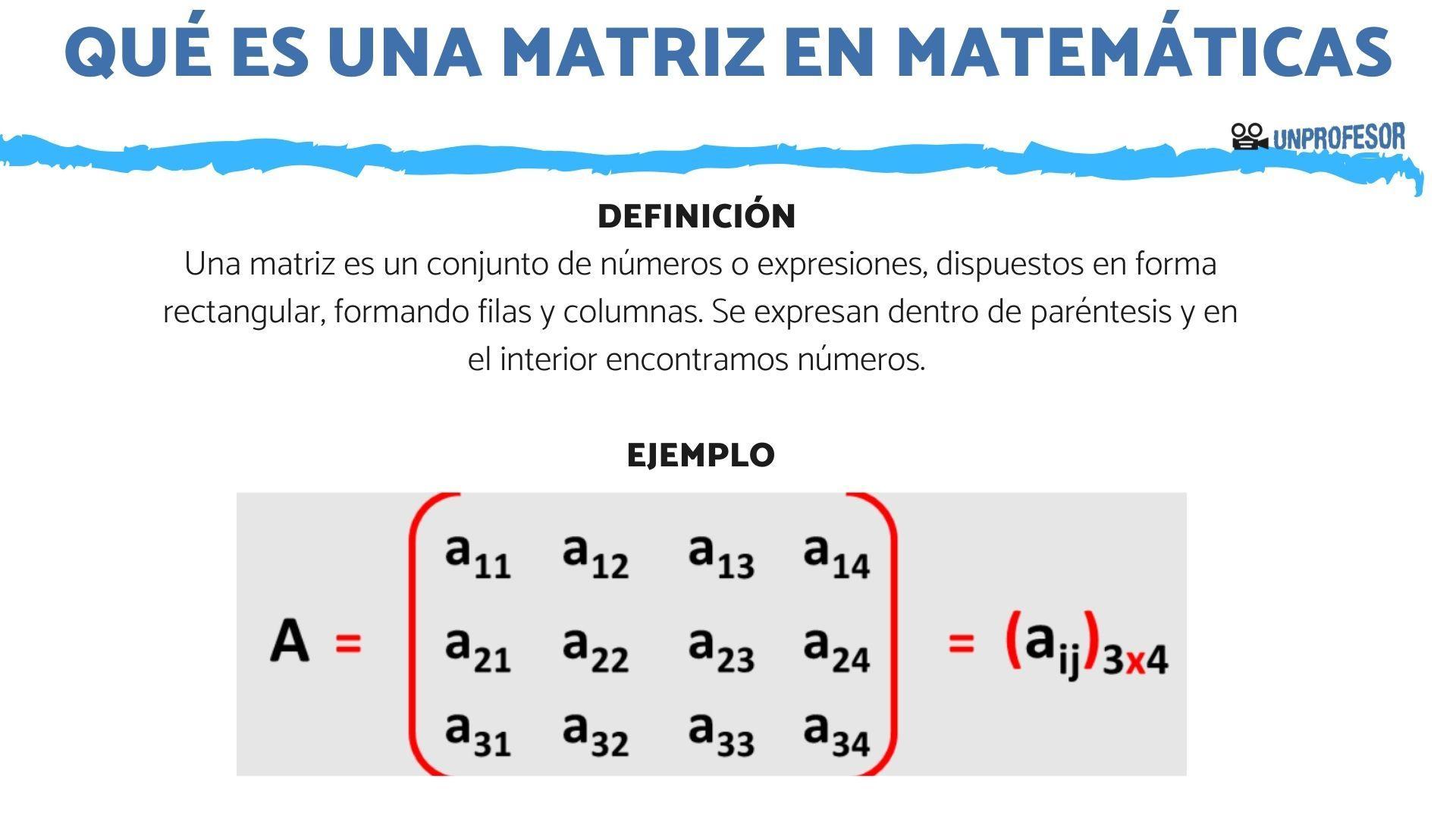
Las matrices son tablas rectangulares o cuadradas que tienen datos, más comúnmente conocidos como elementos, que se encuentran ordenados en filas y columnas. Las filas son las líneas que son horizontales y las columnas son las líneas verticales de toda matriz. Una matriz que está compuesta por m filas y n columnas se dice que es una matriz m x n, donde m y n son las dimensiones de la misma.

Ejemplo

Por ejemplo, si tenemos la matriz A de 3x2, sabemos que tendrá tres filas y dos columnas, entonces:

ab

A=cd

ef

Las matrices pueden estar compuestas por números, letras o expresiones.

Para poder nombrar cada uno de los elementos que componen una matriz A, donde los elementos son variados, se utiliza un subíndice doble para indicar en qué fila y columna está ubicado, es decir si una matriz de 6x5 o de seis filas y cinco columnas, tiene un elemento en la fila tres y columna cuatro, el elemento se nombra como a34.

Teniendo en cuenta el concepto de matrices que vimos anteriormente. Aquí te dejamos una lista con las propiedades de las matrices.

Dimensiones

Toda matriz está caracterizada por las dimensiones que posee, es decir por la cantidad de filas y columnas que la componen. Cada una está formada por m columnas y n filas, y se dice que la matriz es de dimensiones mxn. Por ejemplo, la matriz B de 4x2, tiene cuatro filas y dos columnas y se ve de la siguiente forma:

• ab
• B=cd
• ef
• gh

Igualdad

La igualdad es otra de las propiedades de las matrices. Para que dos matrices se consideren iguales deben tener la misma dimensiones y cada uno de sus elementos ser iguales. Por ejemplo, las matrices A y B son iguales ya que todos sus elementos y dimensiones son iguales. Son dos matrices 3x2.

• 1212
• A=34B=34
• 5656

Suma y resta de matrices

Dos matrices pueden sumarse o restarse si poseen el mismo tamaño, es decir las mismas dimensiones, y se suman o restan los elementos que ocupan el mismo lugar en cada una de las matrices, es decir que como resultado se obtiene una matriz también del mismo tamaño. Por ejemplo, si tenemos la matriz A 2x3 y B 2x3, podemos sumarla y obtenemos una matriz nueva que también será 2x3.

• A= 231B=5-1-2
• -3245 3-4
• A + B = 231+5-1-2
• -3245 3-4
• A + B = 2 + 53 + (-1)1 + (-2)
• -3 + 5 2 + 34 + (-4)
• A + B = 7 2 -1
• 2 5 0

Multiplicación por un escalar

Una multiplicación por un escalar, implica multiplicar una matriz por un número y se obtiene una matriz con las mismas dimensiones. El producto que se realiza es el del número o escalar por cada uno de los elementos de la matriz. Por ejemplo, si tenes la matriz A 2x4 y la queremos multiplicar por el número -2 obtenemos:

• A =213-1
• 14-21
• -2 x A = -2x2-2x1-2x3-2x-1
• -2x1-2x4-2x-2 -2x1
• -2 x A = -4 -2-62
• -2 -8 4-2

Multiplicación entre dos matrices

La multiplicación entre dos matrices es otra de las propiedades de las matrices. Puede realizarse únicamente si la cantidad de columnas que tiene la primera matriz es igual a la cantidad de filas que posee la segunda. La dimensiones de la matriz resultado tendrá la cantidad de filas de la primera matriz con la cantidad de columnas de la segunda matriz.

El producto entonces se realiza multiplicando cada elemento de la columna de la primera matriz por cada elemento de la fila de la segunda matriz y sumándolos. Por ejemplo, si tenemos dos matrices que son A 2x3 y B 3x1. Como A tiene tres columnas y B tiene tres filas, se puede realizar la multiplicación entre ellas.

• A= 21-2B= -3
• -134-1
• 2
• A x B = 2x(-3) + 1x(-1) + (-2)x2 = -6 - 1 - 4
• (-1)x(-3) + 3x(-1) + 4x2 3 - 3 + 8
• A x B = -11
• 8
• El resultado es una matriz 2x1 con dos filas y una columna.

Transposición

Para transponer una matriz se deben intercambiar las filas y las columnas, es decir si una matriz tiene dimensiones m x n entonces su transpuesta tendrá dimensiones n x m. Por ejemplo, tenemos la matriz A de 3x2 su transpuesta será de At de 2x3.

• 54
• A=-23
• -78
• La transpuesta de A sería At
• At=5-2-7
• 438

Determinante de una matriz

El determinante de una matriz tiene muchas aplicaciones, y es un valor numérico que se obtiene cuando las matrices son cuadradas, es decir que tiene la misma cantidad de columnas y filas.

Inversa de una matriz

Las matrices cuadradas pueden invertirse. La inversa de una matriz multiplicada por la matriz original debe dar como resultado la matriz IDENTIDAD. Aquí te contamos cómo calcular una matriz inversa.

Rango de una matriz

El rango de toda matriz es el máximo número de filas o columnas que son linealmente independientes. Tiene aplicaciones para resolver sistemas lineales de ecuaciones.

Traza

La traza de las matrices que son cuadradas es la suma de los elementos de sus diagonales. Propiedad que se utiliza en demostraciones y operaciones.

Si esta lección de propiedades de las matrices te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Cuáles son las propiedades de las matrices, te recomendamos que entres en nuestra categoría de Álgebra.