Qué son los números racionales: ejemplos

Los números racionales son uno de los conjuntos numéricos que se utilizan en matemáticas. Estos números son aquellos que se representan como una división entre dos números enteros, es decir son las ya conocidas fracciones. Recordemos que una fracción es el cociente entre dos números, a/b donde a es el numerador y b el denominador siempre distinto de cero. En esta otra lección te descubrimos los diferentes tipos de fracciones.

Entonces bien, los números racionales son todos aquellos números que se representan a partir del cociente entre dos números que son enteros.

Se llaman racionales ya que proviene de “razón” que es el cociente entre dos números. Existen infinitos números racionales, porque las combinaciones entre los números enteros que también son infinitos no terminan, y a su vez cada número racional puede representarse por una fracción equivalente que también es otro número racional.

Ejemplos de números racionales

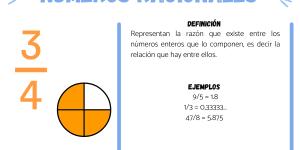
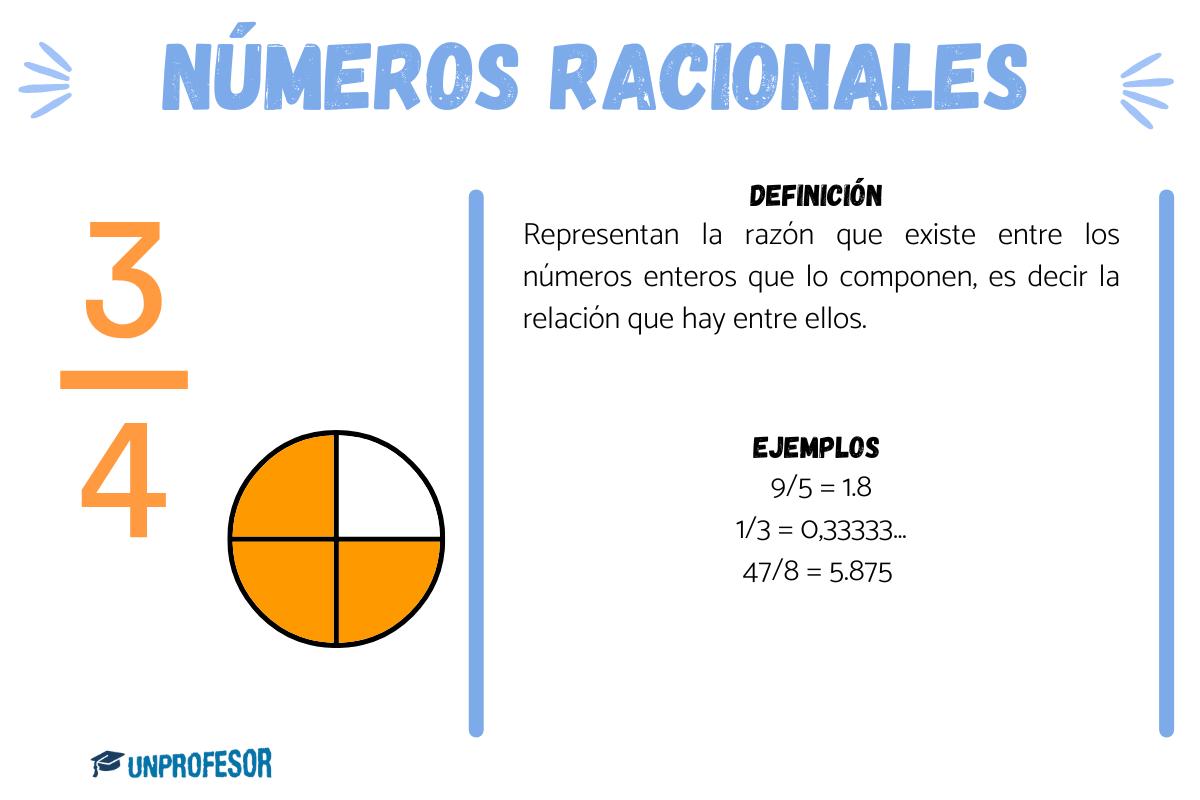
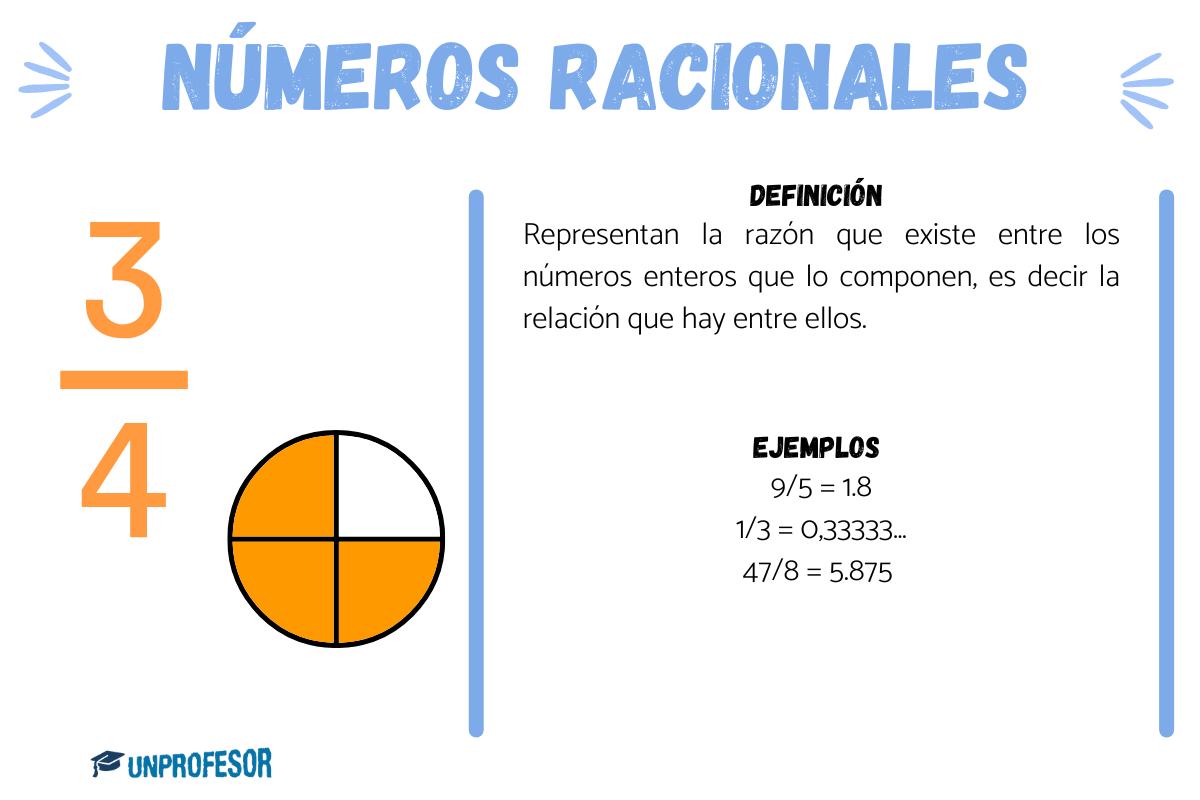
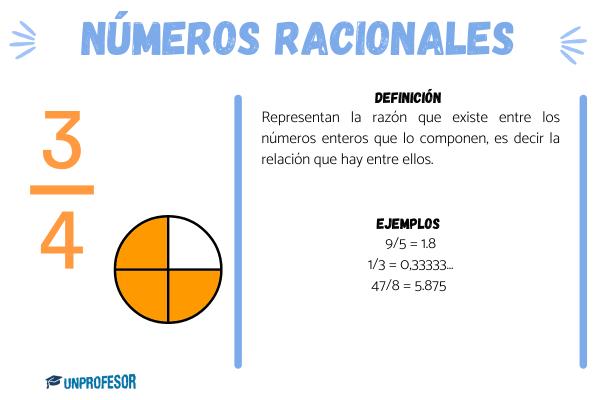
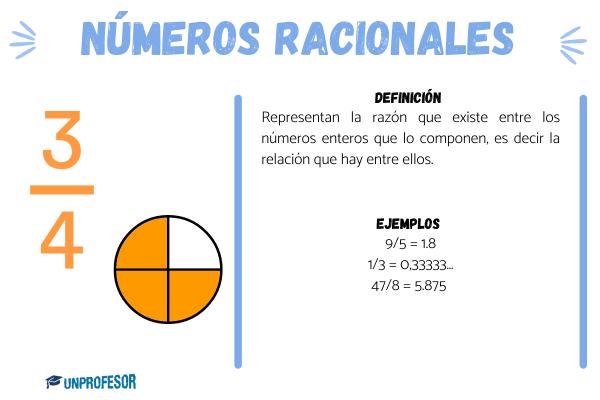
Pueden ser: 9/5, 1/3, 47/8, -1/9, 26/7. Cuando realizamos las divisiones obtenemos:

• 9/5 = 1.8
• 1/3 = 0,33333…
• 47/8 = 5.875
• -1/9 = -0.1111….
• 26/7 = 3,7142857142857…..

(los puntos suspensivos indican que los decimales siguen infinitamente)

Aquellos números que no pueden representarse como el cociente entre dos números enteros se llaman números irracionales. Estos números son aquellos que tienen cifras decimales infinitas NO periódicas, es decir NO se repiten y por lo tanto no pueden representarse como una fracción.

Los números racionales pueden dar como resultado un número entero, un número con decimales “exacto” o un número con decimales periódicos.

• Entero: es cuando el resultado de la división da como resultado un número que es entero, es decir que la división no tiene resto. Por ejemplo, 8/4 = 2, o 9/3 = 3 o 25/25 = 1.
• Decimal exacto: es cuando el resultado tiene una cantidad de decimales finitos, es decir que se conoce la cantidad exacta de decimales que tiene. En los ejemplos que vimos anteriormente estos números son, 9/5 = 1.8 o 47/8 = 5.875, los decimales son conocidos ya que no hay infinitos.
• Decimal periódico: es cuando el resultado tiene infinitos decimales que se repiten de alguna manera, es decir, se repite un número decimal infinitamente, o dos números decimales, o tres o más, pero siempre es la misma cifra la que continúa. En el ejemplo que vimos antes estos números son, 1/3 = 0.3333… donde el número 3 decimal se repite infinitamente, o -1/9 = -0.1111…. donde 1 decimal se repite, o 26/7 = 3,7142857142857….. donde se repite 714285 infinitamente.

Los conjuntos numéricos son aquellos números que utilizamos normalmente y que se encuentran dentro de un grupo al que pertenecen. A su vez, están contenidos dentro de otros grupos que abarcan mayor cantidad de números.

En este caso, hablamos de los números racionales que van a contener a los conjuntos numéricos que ya conocemos que son los enteros (Z) y los naturales (N). Al conjunto de los números racionales se los nombra con la letra Q mientras que al conjunto de los números irracionales con la letra I.

Entonces podemos plantear un diagrama donde vemos que los números naturales están contenidos dentro de los números enteros. A su vez los números enteros están contenidos dentro de los números racionales, y los números irracionales son un conjunto numérico aparte, que más adelante ya veremos en qué conjunto numérico está contenido.

• Números Racionales (Q) → Números Enteros (Z) → Números Naturales (N)
• Números Irracionales (I)

Los números racionales representan la razón que existe entre los números enteros que lo componen, es decir la relación que hay entre ellos. A su vez, cada uno de estos números pueden representarse como una fracción equivalente manteniendo la misma relación, por lo tanto existen infinitas combinaciones. Por ejemplo:

2/1 = 4/2 = 6/3 = 8/4 = 10/5 = 12/6 = 14/7 = …… = 2

o

6/11 = 12/22 = 18/33 = 24/44 = …. = 0,545454…….

o

1/9 = 2/18 = 3/27 = 4/36 = ….. = 0.11111….

Debemos tener en cuenta que, entre dos números enteros, existen una cantidad infinita de números racionales y también irracionales. Por ejemplo, entre los enteros 1 y 2, existen los números 1.4, 1.589, 1.6666…, que son racionales, pero también existe Raíz cuadrada (2) que es irracional.

Una característica o propiedad de los números racionales es que cuando se suma, resta, multiplica o divide dos números racionales siempre se obtiene un número racional como resultado. No así, cuando se aplica una raíz ya que podemos tener como resultado tanto un número racional como un número irracional.

En esta otra lección te descubrimos la diferencia entre números racionales e irracionales.

Si deseas leer más artículos parecidos a Qué son los números racionales: ejemplos, te recomendamos que entres en nuestra categoría de Aritmética.