Diferencia entre los números racionales e irracionales


En esta nueva lección de unProfesor nos complace traerte un tema muy importante dentro del mundo de las matemáticas: en esta lección veremos la diferencia entre los números racionales e irracionales. Por tal motivo, comenzaremos por presentar una breve descripción de cada uno de estos números, para después resaltar sus diferencias más importantes. Como es costumbre para nosotros, estaremos apoyando la explicación teórica con algunos ejemplos prácticos, al igual que con el video de la profesora Claudia López que servirá de complemento en esta lección.
Principales diferencias entre números racionales e irracionales
La diferencia entre los números racionales y los números irracionales es bastante evidente.
- En primer lugar, y quizás más importante, se encuentra el hecho de que, mientras los números racionales pueden ser expresados en forma de fracción, los números irracionales no pueden ser expresados de esta manera.
- Los números racionales son cantidades que pueden tener un periodo en el decimal, o decimal finito y limitados.
- En el caso de los números irracionales, sus decimales tienden al infinito, es decir, que no podemos representarlos en una fracción.
Estas serían las dos mayores diferencias entre los números racionales e irracionales. En este aspecto son completamente contrarios (como efectivamente se aprecia en los siguientes apartados).

Qué son los números racionales
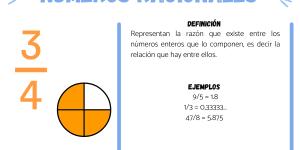
Los números racionales son fracciones que pueden formarse a partir a números enteros y reales. Esto quiere decir que los números racionales son números reales que pueden expresarse también como fracción, ya que podemos calcular o conocer, tanto el numerador como el denominador.
El nombre de racionales es la traducción del inglés, rationals, que hace referencia a ratio, es decir fracción. Entonces, sabiendo que los números racionales se asocian a una ratio, será más fácil recordarlos.
Racional = Rational = Ratio = Fracción => Sí podemos expresarlos como fracción de dos números enteros.
Como podemos observar en el siguiente esquema, los números reales se dividen entre números irracionales y números racionales, los cuales pueden reducirse a números enteros y estos a números naturales.
En resumidas cuentas, para fines teóricos, podemos afirmar que un número es racional sí podemos expresarlo en forma de fracción.

Qué son los números irracionales
Por otro lado, tenemos a los números irracionales. Este tipo de números son números reales que no pueden ser expresados de manera exacta, ni de manera periódica. Esto significa que los números irracionales, no pueden ser expresados en forma de fracción porque no conocemos, o no podemos calcular, el numerador o el denominador.
El nombre de racionales es la traducción del inglés, rationals, que hace referencia a ratio, es decir fracción. Entonces, sabiendo que los números racionales se asocian a una ratio, será más fácil recordarlos.
Irracional = Irrational = Irratio = No Ratio = No Fracción => No podemos expresarlos como fracción de dos números enteros.
Más adelante, en los siguientes apartados, daremos algunos ejemplos de números irracionales para que este aspecto teórico se aprecie con mayor facilidad.

Ejemplos de números racionales
Ya hemos visto la teoría y concepto de estos dos números, ahora vamos a continuar con algunos ejemplos para que puedas observar la diferencia entre los números racionales e irracionales de forma más clara.
En el caso de los números racionales, no hay demasiado misterio. Cualquier número que pueda ser expresado en fracción es un número racional. Por ejemplo:
48 es un número racional, porque puede expresar como fracción.
Otro ejemplo un poco más complejo puede ser 3,5. Este número también es racional, ya que se puede expresar como 7 / 2 que es una fracción, por lo tanto es racional. Sabemos su numerador y denominador, ya que tiene un decimal finito.
Ejemplos de números irracionales
Ahora bien, en el caso de los números irracionales, la diferencia se ve muy clara, pero hay que estar atentos igualmente.
Un número irracional por excelencia sería el número 𝝿 (Pi). Sabemos que este número equivale a 3,1415926… hasta el infinito. Es decir, que no tiene un decimal que conocemos, ya que no es finito; por lo tanto, no podemos expresarlo en forma de fracción.
Otro buen ejemplo de un número irracional serían las raíces. Por ejemplo √3, es un número irracional porque sus decimales tienden al infinito y no podemos expresarlo en una fracción definida. Sin embargo, no todas las raíces son números irracionales; las raíces que pueden calcularse y su resultado es un número exacto, se consideran números racionales.
Está el caso de √4, sabemos que √4 = 2; por lo que sí se puede expresar en forma de fracción, lo que significa que es un número racional.
El objetivo de este último ejemplo, es resaltar el hecho de que no necesariamente si un número es raíz, automáticamente se trata de un número irracional, cada caso es distinto. Como hemos dicho antes, lo que define a un número racional o irracional, es si en definitiva puede expresarse o no en forma de fracción.
Esperamos que esta lección te haya sido de ayuda para este tema y como siempre, sabes que puedes contar con todo el material de unProfesor que está disponible en nuestra página, para este o cualquier otra asignatura con la que necesites un apoyo extra. Te seguimos animando en tus estudios y adelante.
Si deseas leer más artículos parecidos a Diferencia entre los números racionales e irracionales, te recomendamos que entres en nuestra categoría de Aritmética.