Tipos de fracciones y ejemplos

Cuando hablamos de fracción, nos referimos a la idea de que estamos queriendo representar ciertas partes de un todo. Esto quiere decir que estamos realizando una división en partes iguales y que cada una de ellas es una “fracción” del entero, es decir del total.

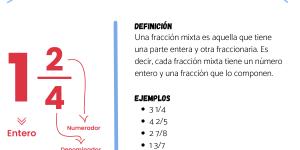
Las fracciones están compuestas por dos términos separados por una línea o barra que denota la división. El término que se ubica en la parte superior de la línea se denomina numerador mientras que el término ubicado en la parte inferior es el que llamamos denominador.

El denominador expresa en cuántas partes se divide el entero, mientras que el numerador marca cuántas partes de ese entero queremos utilizar.

Por ejemplo, si tenemos la fracción 2/7 podemos decir que queremos utilizar 2 partes de un total dividido en 7. En otras palabras, el entero se divide en 7 partes iguales y utilizaremos 2 de ellas.

En matemáticas se pueden realizar diversos tipos de operaciones con fracciones, entre ellas la suma, resta, multiplicación, división, potencia y muchas más. En este vídeo te dejamos operaciones con fracciones para que practiques en casa.

Incluso las fracciones pueden simplificarse, es decir puede dividirse tanto numerador como denominador por el mismo número y entonces así, obtener una nueva fracción que será equivalente a la anterior, pero con números más pequeños.

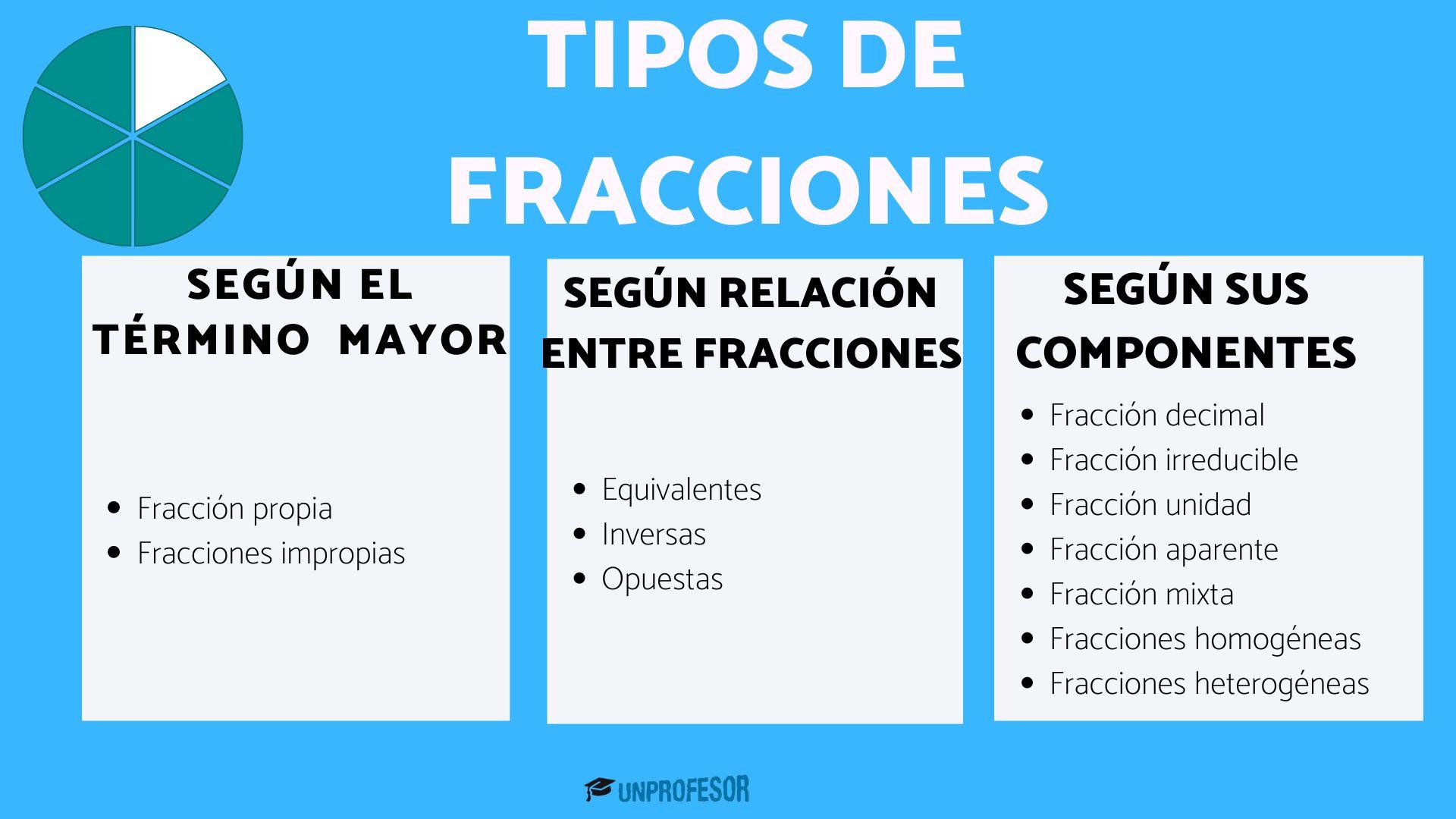
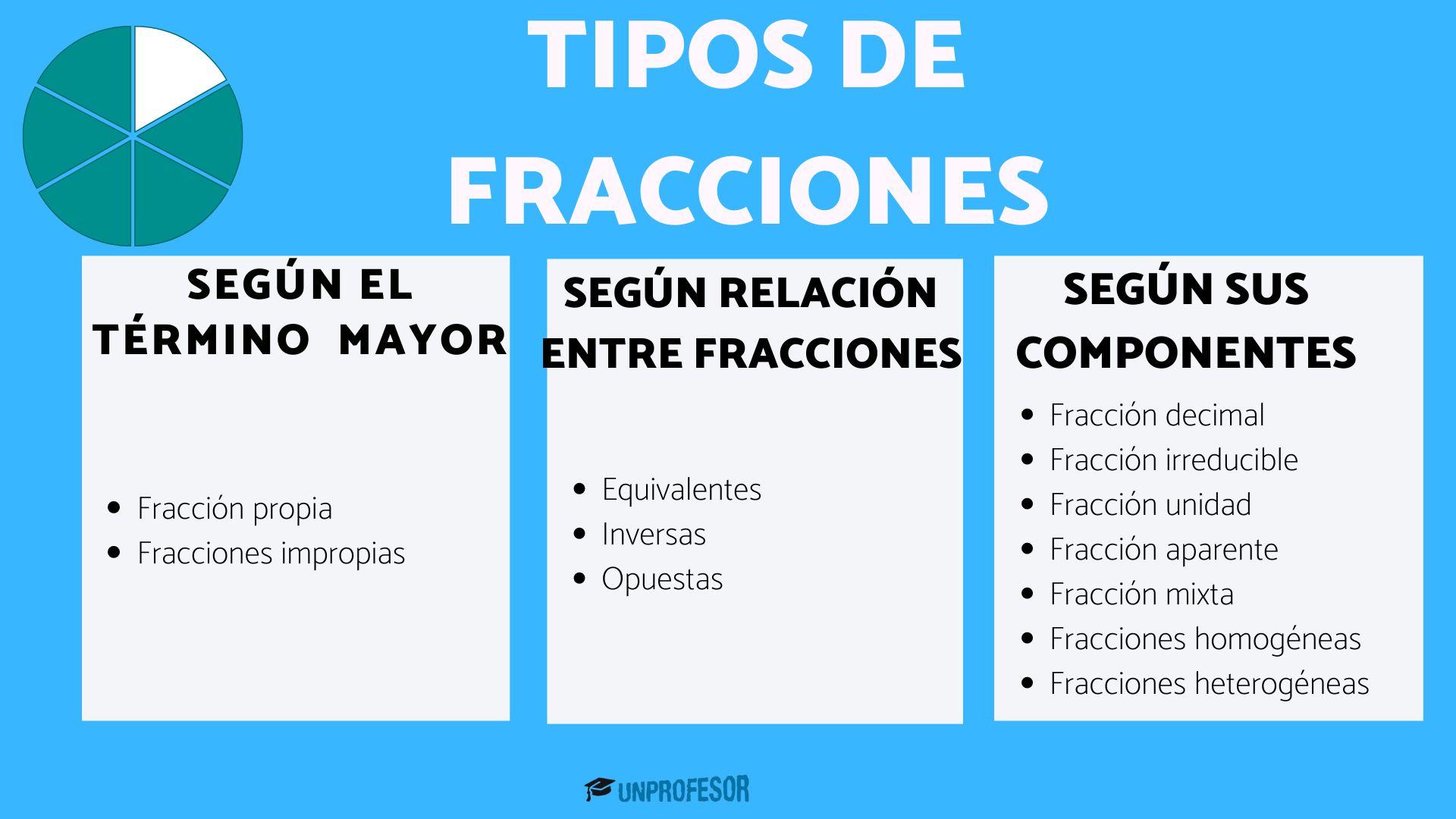
Las fracciones se pueden clasificar de acuerdo a diferentes criterios como por ejemplo, la diferencia que existe entre numerador y denominador o la relación que hay entre dos o más fracciones. Aquí te dejamos los tipos de fracciones que existen.

Según cuál se sus términos es mayor

Dependiendo si el numerador o denominador es mayor que el otro, podemos clasificar las fracciones en:

• Fracción propia: el denominador es un número mayor que el numerador. Por ejemplo: 4/9, 5/12, 6/15, 3/7, etc.
• Fracciones impropias: el numerador es un número mayor que el denominador. Por ejemplo: 6/3, 18/5, 25/4, 10/6, etc.

En el caso de las fracciones propias, siendo el numerador menor al denominador, decimos que tomamos una parte del entero, pero con las fracciones impropias, al ser mayor el numerador que el denominador, podemos deducir que no bastará con una parte de un entero, sino que necesitaremos más de uno para poder utilizar las partes que necesitamos.

Según la relación entre fracciones

De acuerdo a la relación que pueda existir entre dos o más fracciones podemos encontrar estos 3 tipos de fracciones:

• Equivalentes: las fracciones equivalentes, son aquellas que al realizar la división entre las partes de cada una de ellas, arroja el mismo resultado en ambos, a pesar de que los términos que las componen sean diferentes. Por ejemplo: 4/8 y 8/16 podemos pensar que una fracción es el doble de la otra y darnos cuenta a simple vista, o hacemos 4 dividido 8 y 8 dividido 16 y veremos el mismo resultado. 4/8 = 1/2 y 8/16=1/2 por lo tanto son equivalentes.
• Inversas: dos fracciones son inversas cuando el numerador de una es igual al denominador de la otra y viceversa, es decir tienen los mismos componentes pero ubicados de forma “inversa”. Por ejemplo: 3/8 y 8/3 o 4/7 y 7/4. En estos casos, cuando las fracciones son inversas y se realiza la multiplicación entre ellas, el resultado SIEMPRE es igual a 1. 3/8 x 8/3 = 1.
• Opuestas: dos fracciones son opuestas cuando tienen los mismos componentes, pero una de ellas tiene el signo contrario. Es decir, son dos fracciones iguales salvo que una es positiva y la otra negativa. Por ejemplo: 2/9 y -2/9 o 6/15 y -6/15. En estos casos, cuando las fracciones son opuestas y se realiza la suma entre ellas, el resultado SIEMPRE es 0. 2/9 + -2/9 = 0.

Según sus componentes

Otro de los tipos de fracciones que dependen de cuáles sean los términos que la componen pueden ser las siguientes:

• Fracción decimal: estas fracciones son las que como denominador tienen a 10 o una potencia de 10. Es decir, cualquier múltiplo de 10. Por ejemplo: 4/10, 39/100, 455/1000, etc. Estas fracciones son muy sencillas de resolver, incluso si tenemos números decimales exactos, podemos realizar el pasaje a fracción sin ninguna dificultad.
• Fracción irreducible: estas fracciones son aquellas cuyo numerador y denominador no poseen ningún divisor común y por lo tanto no pueden simplificarse. Es decir, que es la fracción más pequeña a la que puede llegarse. Por ejemplo: 13/8, 4/9, 25/4, etc.
• Fracción unidad: estas fracciones representan el todo, es decir su numerador y denominador son iguales por lo tanto están expresando la unidad o entero. Es sencillo de comprender, ya que la división entre dos números que son iguales siempre arroja como resultado el número 1, y por lo tanto el entero. Por ejemplo: 78/78, 9/9, 34/34, etc.
• Fracción aparente: estas fracciones son aquellas que al realizar la división entre numerador y denominador obtenemos como resultado un número entero, esto quiere decir que ambos son múltiplos. Por ejemplo: 8/4, 9/3, 6/2, etc.
• Fracción mixta: estas fracciones son aquellas que tienen una parte entera y otra fraccionaria, es decir que representan los enteros y la parte una parte que falta. Estas fracciones pueden representarse por las fracciones impropias, ya que estamos hablando de más de un entero y una parte, entonces podemos deducir que el numerador será mayor al denominador. Por ejemplo: 3 1/4, 6 1/2 , 2 3/4 , etc.Para poder escribir la mayor mixta como una impropia, la forma de realizarlo es la siguiente: se multiplica el denominador por el entero y luego se le suma el numerador de la fracción. Ese resultado será el numerador de nuestra fracción impropia, mientras que el denominador seguirá siendo el mismo que antes. Ejemplo:3 1/4 = (3 x 4 + 1) / 4 = (12 + 1) / 4 = 13/4. Entonces la fracción mixta 3 1/4 será representada por su fracción impropia como 13/4.
• Fracciones homogéneas: son aquellas fracciones cuyo denominador es el mismo. Es decir, su denominador es igual para todas. Por ejemplo: 1/8, 5/8, 14/8, 25/8, etc. Todas tienen un denominador igual a 8, entonces el entero se dividirá siempre en 8 partes iguales.
• Fracciones heterogéneas: son aquellas fracciones cuyo denominador es diferente. Es decir, no poseen un mismo denominador. Por ejemplo: 4/7, 9/3, 5/4, etc.

Para que termines de comprender esta lección sobre los tipos de fracciones, aquí tienes un ejercicio y las soluciones están más abajo.

Ejercicio 1

En este primer ejercicio, les proponemos clasificar las siguientes fracciones según corresponda para ver si logran recordar lo que leyeron anteriormente sobre los tipos de fracciones que existen.

• 8/4
• 7/3
• 13/15 y 15/13
• 2 3/4
• 7/100
• 4/5 y 6/9
• 2/6
• 2/9 y 8/9
• 4 6/7
• -7/12 y 7/12
• 27/27
• 40/10.000
• 2/9

Soluciones

• 8/4 aparente
• 7/3 impropia
• 13/15 y 15/13 inversa
• 2 3/4 mixta
• 7/100 decimal
• 4/5 y 6/9 heterogéneas
• 2/6 propia
• 2/9 y 8/9 homogéneas
• 4 6/7 mixta
• -7/12 y 7/12 opuestas
• 27/27 unidad
• 40/10.000 decimal
• 2/9 irreducible

Aquí te contamos cómo leer fracciones.

Para descubrir si entendieron cuáles son las clasificaciones que pueden tener las fracciones, les proponemos que decidan si son verdaderas o falsas las siguientes afirmaciones, y deberán justificar las que son falsas.

1. 16/5 es una fracción irreducible
2. 4/9 y -4/9 son fracciones inversas
3. 9/3 es una fracción aparente
4. 4 2/9 es una fracción mixta
5. 100/3 es una fracción decimal
6. 12/4 y 16/4 son fracciones homogéneas
7. 7/6 es una fracción propia
8. 6/9 es una fracción irreducible
9. 108/108 es una fracción unidad

Soluciones

1. 16/5 es una fracción irreducible. Verdadero.
2. 4/9 y -4/9 son fracciones inversas. Falso, son fracciones opuestas ya que son iguales pero con el signo contrario.
3. 9/3 es una fracción aparente. Verdadero.
4. 4 2/9 es una fracción mixta. Verdadero.
5. 100/3 es una fracción decimal. Falso, las fracciones decimales tienen un múltiplo de 10 como denominador, no en el numerador.
6. 12/4 y 16/4 son fracciones homogéneas. Verdadero.
7. 7/6 es una fracción propia. Falso, es una fracción impropia, ya que el numerador es mayor que el denominador.
8. 6/9 es una fracción irreducible. Falso, puede reducirse ya que ambos números son múltiplos de 3 por lo tanto pueden dividirse por este, quedando la fracción como 2/3.
9. 108/108 es una fracción unidad. Verdadero.

En el siguiente ejercicio proponemos que repasen el concepto de fracciones mixtas e impropias. Por lo tanto deberán escribir las siguientes fracciones mixtas en su fracciones impropias.

• 5 1/3
• 3 2/7
• 2 5/8
• 6 1/2
• 1 4/6

Soluciones

• 5 1/3 Tenemos 5 enteros y 1 parte de 3 por lo tanto realizaremos la cuenta:

5 1/3 = (5 x 3 + 1) / 3 = (15 + 1) / 3 = 16/3.

• 3 2/7 Tenemos 3 enteros y 2 partes de 7 por lo tanto hacemos la cuenta:

3 2/7 = (3 x 7 + 2) / 7 = (21 + 2) / 7 = 23/7

• 2 5/8 Tenemos 2 enteros y 5 partes de 8 por lo que realizamos la cuenta:

2 5/8 = (2 x 8 + 5) / 8 = (16 + 5) / 8 = 21/8

• 6 1/2 Tenemos 6 enteros y 1 parte de 2 entonces resolvemos la cuenta:

6 1/2 = (6 x 2 + 1) / 2 = (12 + 1) / 2 = 13/2

• 1 4/6 Tenemos 1 entero y 4 partes de 6 entonces realizamos la cuenta:

1 4/6 = (1 x 6 + 4) / 6 = (6 + 4) / 6 = 10/6

Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Tipos de fracciones y ejemplos, te recomendamos que entres en nuestra categoría de Aritmética.