Cómo sacar el diámetro de un círculo

Una de las partes más importantes del círculo es el diámetro. El diámetro de un círculo es la medida de la semirrecta trazada desde cualquiera de los puntos de la circunferencia hacia otro punto y que pasa por el centro del círculo.

Como la medida del diámetro siempre es la misma, entonces podremos dividir SIEMPRE en dos partes iguales a cualquier círculo.

Por otro lado, podemos asegurar que el diámetro es la suma de dos radios de un círculo. Osea que si poseemos la medida del radio, pero NO del diámetro, multiplicamos por dos el radio y obtenemos su longitud.

La razón entre la circunferencia de un círculo y su diámetro es el número π.

Entonces si C es la circunferencia de un círculo y d su diámetro, tenemos:

C/d = π

Imagen: Diferenciador

Para calcular el diámetro de un círculo, debemos tener como dato alguna de sus otras medidas o dimensiones. Es decir, debemos conocer el radio o la circunferencia.

1-Conociendo el radio

Como vimos anteriormente, el diámetro es el doble del radio, por lo que conociendo el valor de la medida del radio, podemos obtener el diámetro multiplicando a este por dos.

Entonces si r es el radio y d el diámetro:

d = 2 x r

2- Conociendo la circunferencia

Como vimos en el concepto de diámetro, la razón entre la circunferencia y el diámetro es igual a π, por lo tanto despejamos de la ecuación al diámetro y obtenemos el resultado.

• C / d = π
• C / π = d

Ejemplos de cómo sacar el diámetro de un círculo

Sea un círculo de radio 5 cm. Calcula el diámetro.

Sabiendo que el diámetro es dos veces el radio, usamos la fórmula y obtenemos el resultado.

• d = 2 x r
• d= 2 x 5
• d = 10 cm

El diámetro del círculo es de 10 cm.

Sea un círculo de 25 cm de circunferencia. Calcula el diámetro del mismo.

Si conocemos la medida de la circunferencia del círculo, utilizamos la fórmula de la opción dos y calculamos

• C / d = π
• C / π = d
• 25 / π = d
• d = 7,95 cm

Entonces la medida del diámetro es de 7.95 cm

En esta otra lección te contamos cómo sacar el área de un círculo con diámetro.

Un círculo, dentro de la geometría, es una figura que se encuentra delimitada por la circunferencia, siendo ésta la línea que forma el límite o contorno de nuestro círculo. El círculo entonces es el área que forma o contiene a una circunferencia.

Existe entonces una diferencia entre círculo y circunferencia debido a su definición. Mientras que la circunferencia es la línea curva que forma o delimita una figura, el círculo es el área o superficie que se encuentra contenido en esa línea.

Además, podemos decir, que el círculo es una figura de dos dimensiones que se representa mediante una línea curva llamada circunferencia, siendo esta cerrada, y en la cual cualquiera de sus puntos tendrá la misma longitud de distancia con el centro del círculo.

Partes de un círculo

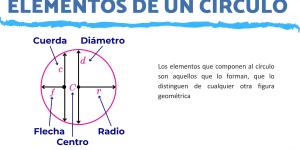
Las partes que forman un círculo son las siguientes:

• Circunferencia: línea curva que delimita al círculo, es decir la frontera del mismo, su contorno.
• Centro: es el punto que se encuentra en el medio de la circunferencia, es decir que posee la misma distancia en todos sus puntos.
• Radio: es la semirrecta que une el centro del círculo con cualquier punto de la circunferencia.
• Diámetro: es la semirrecta que une dos puntos contrarios de la circunferencia y que pasa por el centro del círculo.
• Cuerda: es la semirrecta que une dos puntos cualesquiera de la circunferencia y que NO pasa por el centro. La medida de la cuerda siempre es menor que la medida del diámetro.
• Arco: es una parte de la circunferencia que se mide entre dos puntos cualesquiera de la misma.

Aquí te dejamos ejercicios para que sepas cómo sacar el diámetro de un círculo. Encontrarás también las soluciones para que puedas practicar en casa.

Ejercicio 1

Decir si es verdadero y falso

1. El diámetro de un círculo es la medida de 3 radios.
2. El círculo es la superficie delimitada por la circunferencia.
3. El radio de un círculo es igual a la medida de la cuerda.
4. El diámetro es la línea que pasa por el centro y une dos puntos de la circunferencia.
5. La razón entre la circunferencia y el diámetro es igual a π.
6. Se puede calcular el diámetro de un círculo conociendo la medida del arco.
7. La cuerda y el diámetro son de igual medida.

Solución

1. Falso. El diámetro de un círculo es dos veces el radio.
2. Verdadero.
3. Falso. El radio es la distancia desde cualquier punto de la circunferencia hasta el centro del círculo, mientras que la cuerda es la unión de dos puntos cualquiera de la circunferencia que NO pasan por el centro.
4. Verdadero.
5. Verdadero.
6. Falso. Se puede conocer el diámetro de un círculo conociendo el valor del radio o de la circunferencia.
7. Falso. La medida de la cuerda siempre será menor a la del diámetro.

Ejercicio 2

Calcula.

1. Calcula el diámetro del círculo, siendo el radio de 6 cm.
2. Calcula el diámetro del círculo siendo la circunferencia de 65 cm.
3. Calcula el diámetro del círculo siendo la circunferencia de 32 cm.
4. Calcula el diámetro del círculo, siendo el radio de 14 cm.

Solución

1-Sabiendo que el diámetro es dos veces el radio, usamos la fórmula y obtenemos el resultado.

d = 2 x r

d= 2 x 6

d = 12 cm

El diámetro del círculo es de 12 cm.

2-Si conocemos la medida de la circunferencia del círculo, utilizamos la fórmula de la opción dos y calculamos

C / d = π

C / π = d

65 / π = d

d = 20.69 cm

Entonces la medida del diámetro es de 20.69 cm.

3-Si conocemos la medida de la circunferencia del círculo, utilizamos la fórmula de la opción dos y calculamos

C / d = π

C / π = d

32 / π = d

d = 10.18 cm

Entonces la medida del diámetro es de 10.18 cm.

4-Sabiendo que el diámetro es dos veces el radio, usamos la fórmula y obtenemos el resultado.

d = 2 x r

d= 2 x 14

d = 28 cm

El diámetro del círculo es de 28 cm.

Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Cómo sacar el diámetro de un círculo, te recomendamos que entres en nuestra categoría de Geometría.