Conversión de unidades angulares
En este vídeo os explicaré la conversión de unidades angulares. En el vídeo anterior, hemos visto las unidades angulares de la trigonometría: en grado y los radianes. Es este, vamos a ver cómo convertir de una unidad a la otra.
Los grados y los radianes son dos diferentes sistemas para medir ángulos. Un ángulo de 360° equivale a 2π radianes; un ángulo de 180° equivale a π radianes (recordemos que el número π ≈ 3,14).
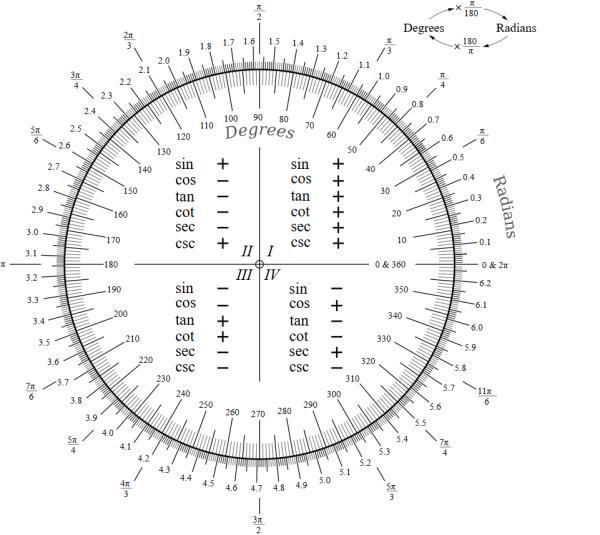
Las equivalencias de los principales ángulos se muestran en las siguientes figuras: Para convertir grados en radianes o viceversa, partimos de que 180° equivalen a π radianes; luego planteamos una regla de tres y resolvemos.
También podéis hacer los ejercicios imprimibles con sus soluciones que os he dejado en la web.
Si deseas leer más artículos parecidos a Conversión de unidades angulares, te recomendamos que entres en nuestra categoría de Trigonometría.
