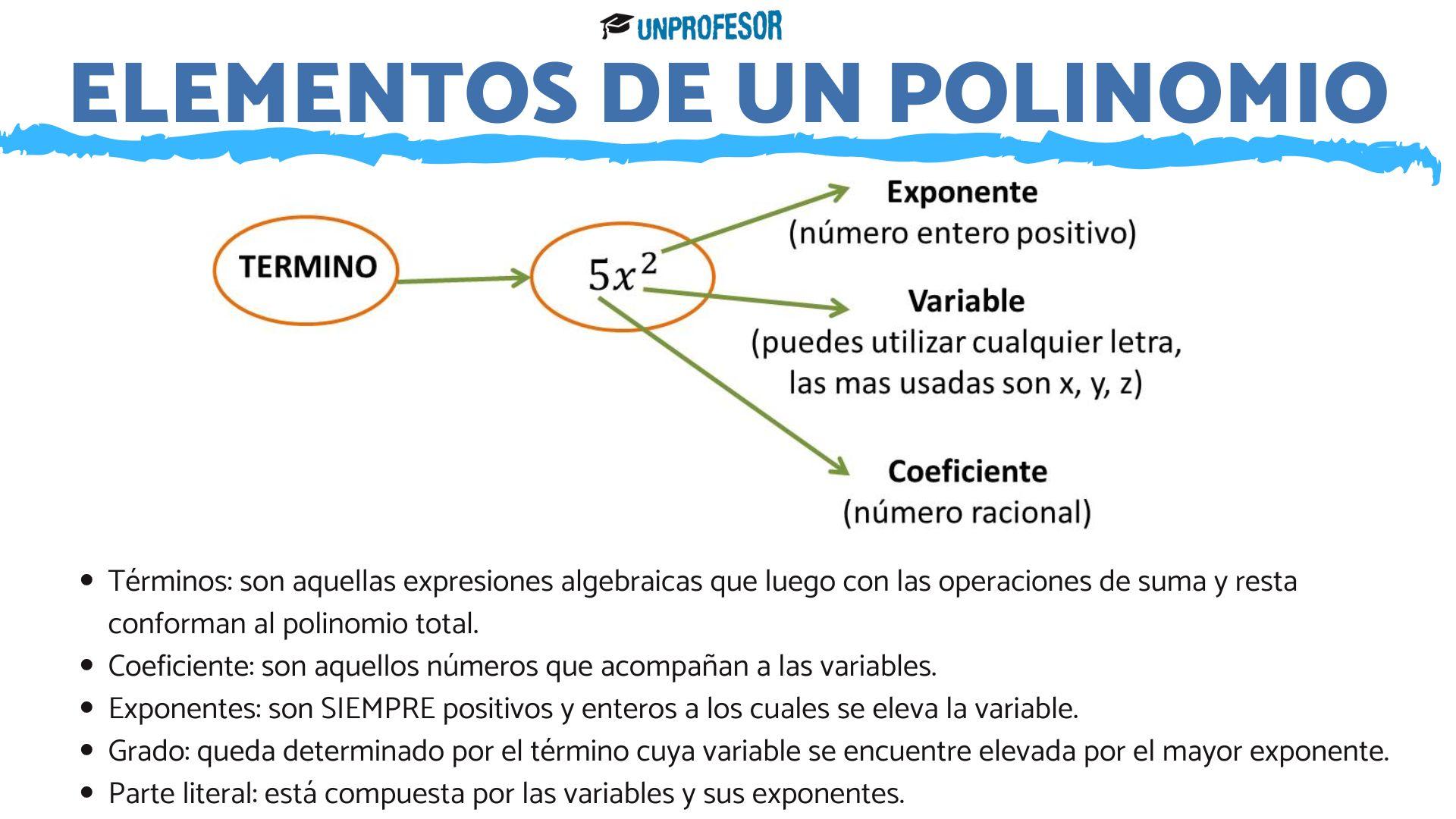
Elementos de un polinomio: ejemplos

Un polinomio es un conjunto de expresiones algebraicas que se unen a partir de operaciones de suma y resta entre varios términos. Los términos que son individuales, son llamados monomios, y son los que forman, a partir de la suma o resta, los polinomios. Es decir, cuando juntamos dos o más monomios, hablamos de un polinomio.

En matemáticas, generalmente en situaciones problemáticas, se utilizan mucho las expresiones algebraicas, es decir un conjunto de letras y números que se unen con suma y resta. Los polinomios son expresiones algebraicas especiales, ya que las letras o variables siempre se encuentran elevadas a un exponente entero que es siempre positivo.

Los polinomios se clasifican según la cantidad de expresiones algebraicas que lo conforman. Si el polinomio está formado por una sola expresión algebraica, entonces se llamará MONOMIO, si el polinomio tiene dos expresiones, se llamará BINOMIO, en cambio sí posee tres expresiones lo denominamos TRINOMIO, a partir de cuatro o más términos simplemente se le denomina POLINOMIO.

Ejemplos de polinomios

Algunos ejemplos de polinomios podrían ser:

• P(x) = 4x⁵ - 7x³ + 2x² + 3
• Q(x) = -3y² - 6y + 5
• R(x) = 12z³ - 5

Los elementos de un polinomio son los siguientes.

Términos de los polinomios

Los términos de un polinomio son aquellas expresiones algebraicas que luego con las operaciones de suma y resta conforman al polinomio total. Es decir, son las expresiones que tienen una variable elevada a un exponente positivo y un coeficiente.

Los términos de varios polinomios pueden ser semejantes si coinciden en la variable y el exponente al cual están elevados sin importar que los coeficientes sean diferentes. Por ejemplo Q(x) = 4y² - 4y + 5 y P(x) = -6y² + y - 9

• Término de mayor grado: el término de mayor grado es aquel cuya variable está elevada al mayor exponente de todos los términos. Es decir, el mayor exponente del polinomio.
• Término independiente: el término independiente es aquel cuya variable se encuentra elevada a la potencia 0, es decir que como su resultado es siempre 1, ya que todo número o variable elevado a la 0 es igual a 1, será el término en el cual figure o sea visible solo el coeficiente. Con esto queremos decir, que el término independiente será sólo un número, no tendrá ninguna variable.

Coeficiente

Los coeficientes de un polinomio son aquellos números que acompañan a las variables. Estos números pertenecen al conjunto de los números racionales y se multiplican por las variables en cada término. Existe un coeficiente que se denomina coeficiente principal y es aquel número que acompaña a la variable que posee mayor exponente, es decir al término que posee mayor grado.

Por ejemplo P(x) = -4x⁵ + 7x³ - 2x - 6. Los coeficientes son -4, 7, -2 y -6. El coeficiente principal es -4.

Exponentes

Los exponentes son otro de los elementos de un polinomio y son SIEMPRE positivos y enteros a los cuales se eleva la variable. Es decir que las variables tendrán una potencia que será un número entero y positivo. No es posible utilizar potencias fraccionarias, por lo tanto las variables nunca podrán estar dentro de una raíz tampoco.

Grado

El grado de un polinomio queda determinado por el término cuya variable se encuentre elevada por el mayor exponente. De esta forma, podemos decir que el polinomio es de grado “tal”. Por ejemplo, si el mayor exponente de un polinomio es una variable elevada a 3, entonces decimos que el polinomio es de grado 3. Si en cambio el mayor exponente es 5, entonces será de grado 5.

• Grado absoluto: el grado absoluto de un polinomio consiste en sumar los exponentes si existen términos con más de una variable, por ejemplo si tenemos 7y²x⁴ entonces el grado absoluto será 6 ya que sumamos 2 + 4 = 6.
• Grado relativo: el grado relativo corresponde a los mayores exponentes de las variables de cada término, por ejemplo si tenemos 2x³y⁵ - 4x⁴y³ entonces el grado relativo de x será 4 y el grado relativo de y será 5.

Parte literal

La parte literal es otro de los elementos de un polinomio. Está compuesta por las variables y sus exponentes, es decir que los coeficientes acompañan a la parte literal en la expresión algebraica.

Por ejemplo si tenemos un monomio 4x⁵ entonces el coeficiente es 4 y la parte literal será x⁵.

Ahora que ya conoces los diferentes elementos de un polinomio, vamos a hablarte sobre estos dos tipos:

• Polinomio ordenado: los polinomios que se encuentran ordenados son aquellos cuyo primer término es el de mayor exponente, luego el menor siguiente y sucesivamente hasta llegar al de menor potencia. Por ejemplo: el polinomio P(x) = 13y³ - 15x² + 4 es un polinomio ordenado, ya que comienza con la potencia 3, siendo el polinomio de grado 3, sigue con exponente 2 y finaliza con el término independiente. Mientras que el polinomio Q(x) = -5x² + 4x⁴ - 7x³ se encuentra desordenado.
• Polinomio completo: Un polinomio es completo cuando posee todas las potencias desde su grado hasta el término independiente, es decir que comienza con el mayor exponente, y contiene todas las potencias que son menores hasta llegar al exponente cero. Por ejemplo, el polinomio P(x) = -5x⁴ + 3x³ - 6x² - 4x + 7 es un polinomio completo.

En esta otra lección te descubrimos los diferentes tipos de polinomios.

Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Elementos de un polinomio: ejemplos, te recomendamos que entres en nuestra categoría de Álgebra.