Tipos de binomios


Los tipos de binomios son los homogéneos, heterogéneos, semejantes e iguales. En unProfesor te lo descubrimos en esta lección fácil con ejercicios y soluciones . En una nueva lección estudiaremos los tipos de binomios. Para ello, comenzaremos recordando qué es un binomio. Seguiremos con los tipos de binomios para terminar con algunos ejemplos y ejercicios de binomios.
Cuáles son los tipos de binomios
- Binomios homogéneos: son aquellos binomios que poseen el mismo grado absoluto.
- Binomios heterogéneos: son aquellos binomios en los que sus términos no tienen el mismo grado absoluto.
- Binomios semejantes: son aquellos binomios cuya parte literal y exponentes son iguales sin tener en cuenta cuales son los coeficientes.
- Binomios iguales: son aquellos binomios en los que todos sus términos son iguales.

Qué es un binomio y ejemplos
Ahora que ya conoces los tipos de binomios, vamos a descubrir su descripciónLos binomios son expresiones algebraicas que están formadas por dos términos, dicho de otra forma son polinomios que poseen únicamente dos términos o dos monomios relacionados entre sí por algún operador matemático de suma o de resta.
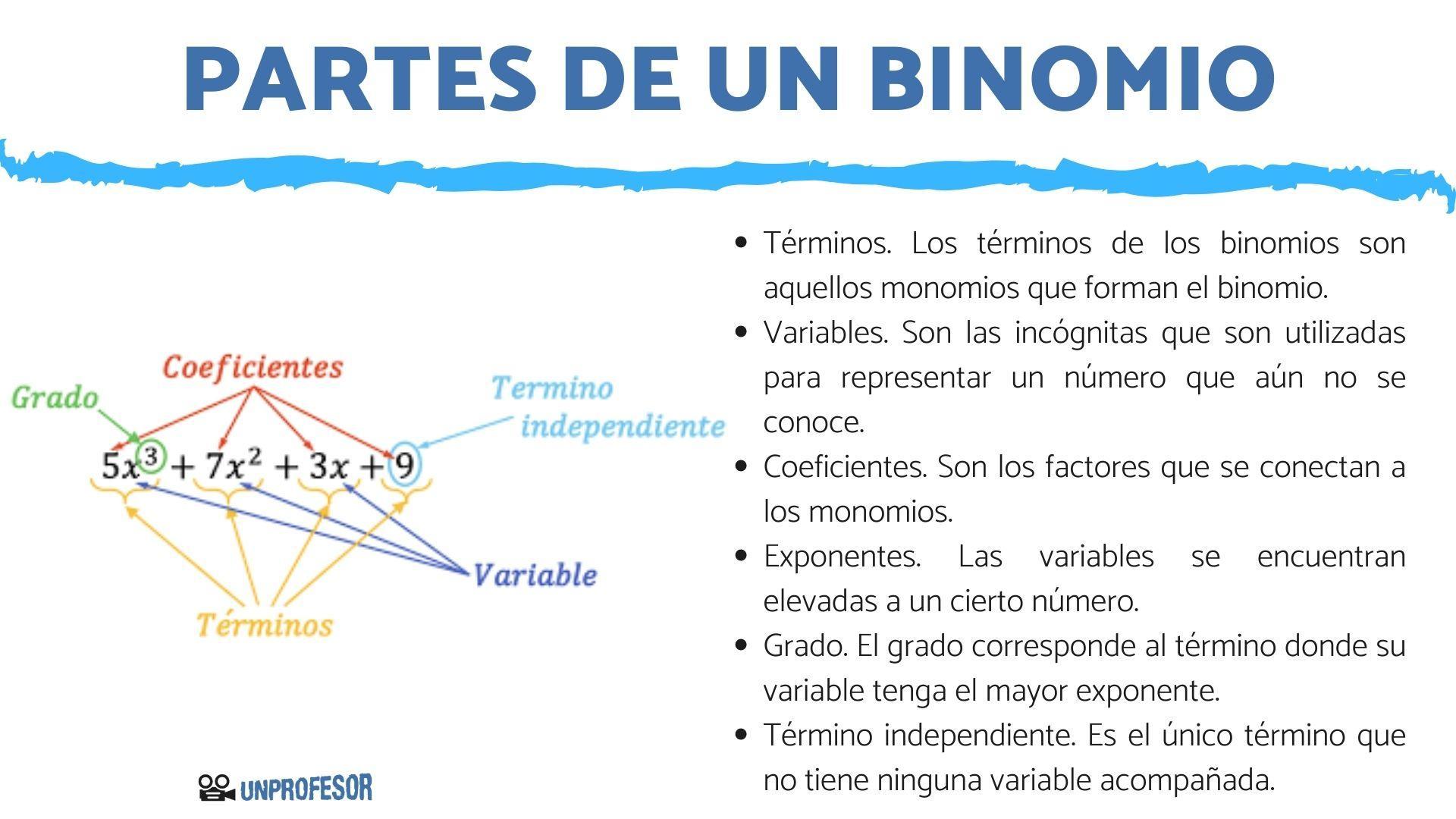
Los elementos de un binomio son como los de cualquier polinomio, y son:
- Términos: son los dos monomios que lo forman
- Coeficiente: son los números que forman los términos algebraicos
- Variables: es la letra o “incógnita” que representa un valor desconocido
- Exponente: el valor al cual la variable está elevada
- Término independiente: número o monomio cuya variable o incógnita no se encuentra presente
- Grado: es el término que mayor grado posee

Operaciones con binomios
Las operaciones que pueden realizarse con los binomios son:
- factorización
- suma
- resta
- división
- multiplicación
Suma o resta de binomios
Para realizar alguna de estas operaciones, se deben juntar los términos que sean semejantes, es decir que posean la misma incógnita y grado, para luego sumarlos o restarlos según el signo que tenga su coeficiente.
Multiplicación
Se pueden utilizar las propiedades asociativa, distributiva y conmutativa sin olvidarse de la regla de los signos. Se pueden multiplicar los términos de un binomio, sin importar el grado que posean.
División
En este caso, se dividen los coeficientes y variables teniendo en cuenta la ley de los exponentes y la regla de los signos de la potencia.
En unProfesor te descubrimos qué es un binomio al cuadrado.
Clasificación de binomios
Ahora que ya conocemos los diferentes tipos de binomios, vamos a dejarte la clasificación de binomios.
Binomio cuadrado perfecto
Un binomio cuadrado perfecto, es la suma o resta de dos términos, elevados al cuadrado. Es decir:
(a+b)2 o (a-b)2
Para resolverlo, utilizamos la fórmula siguiente, teniendo en cuenta sus términos.
“el cuadrado del primero más o menos, el doble del primero por el segundo más el cuadrado del segundo”
- (a+b)2 = a2 + 2 . a . b + b2
- (a-b)2 = a2 - 2 . a . b + b2
Ejemplo
(3+2x)2 =
32 + 2 . 3 . 2x + (2x)2=
9 + 12x + 4x2
(2-x)2 =
22 - 2 . 2 . x + x2=
4 - 4x + x2
Binomio cubo perfecto
Un binomio cubo perfecto, es la suma o resta de dos términos, que se encuentran elevados al cubo. Es decir:
(a+b)3 o (a-b)3
Para resolverlo, utilizamos la fórmula siguiente, teniendo en cuenta sus términos.
“el cubo del primero más o menos, el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más o menos el cubo del segundo”
- (a+b)3= a3 + 3 . a2 . b + 3 . a. b2 + b3
- (a-b)3= a3 - 3 . a2 . b + 3 . a. b2 - b3
Ejemplo
(x+1)3=
x3 + 3 . x2 . 1 + 3 . x . 12 + 13=
x3 + 3 x2 + 3 x + 1
(2x-1)3=
(2x)3 - 3 . (2x)2 . 1 + 3 . 2x . 12 - 13=
8x3 - 12 x2 + 6 x - 1
Diferencia de cuadrados
Una diferencia de cuadrados, es la diferencia del cuadrado de cada uno de sus términos. Es decir:
a2 - b2 = (a-b) . (a+b)
Ejemplo
(2x)2 - 32 = (2x - 3) . (2x + 3)

Ejercicios con binomios con soluciones
Para terminar, te dejamos estos ejercicios con binomios con soluciones.
1) Resolver los siguientes binomios:
- (2y-2)2
- x2 - 42
- (x+2)3
Resultados
- (2y-2)2 = (2y)2 - 2 . 2y . 2 + 22= 4y2 - 8y + 4
- x2 - 42 = (x - 4) . (x + 4)
- (x+2)3= x3 + 3 . x2 . 2 + 3 . x . 22 + 23= x3 + 6 x2 + 12 x + 8
2) Verdadero y falso
Las siguientes afirmaciones son verdaderas o falsas….
- El binomio (y-4)2 puede calcularse como una diferencia de cuadrados
- El binomio (2x)2 - 32 debe calcularse como una diferencia de cuadrados
- El binomio (2x+1)3 es un binomio cuadrado perfecto
- El binomio (4+2y)2 es un binomio cubo perfecto
- El binomio (3x-2)3 es un binomio cubo perfecto
Resultados
- Falso, debe calcularse como un binomio cuadrado perfecto con una resta.
- Verdadero.
- Falso, es un binomio cubo perfecto.
- Falso, es un binomio cuadrado perfecto
- Verdadero.
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.
Si deseas leer más artículos parecidos a Tipos de binomios, te recomendamos que entres en nuestra categoría de Álgebra.