Qué es un triángulo rectángulo y ejemplos

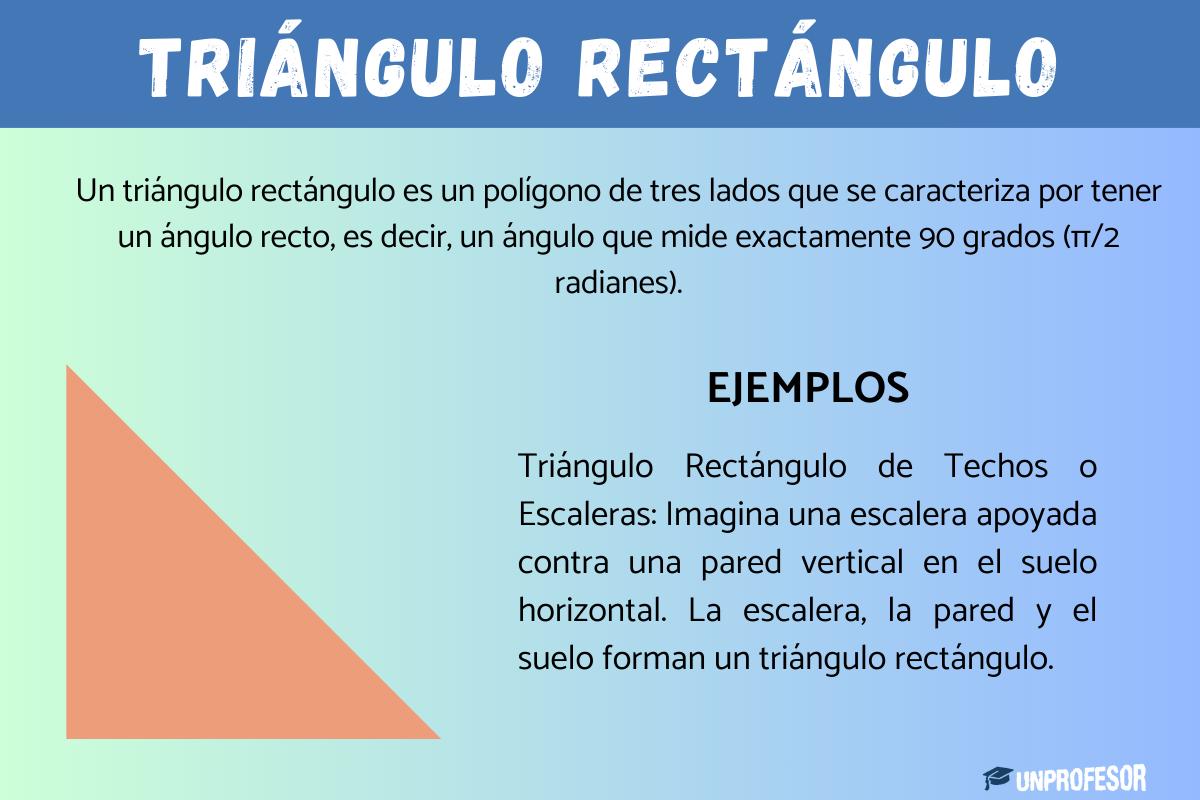
Un triángulo rectángulo es una figura geométrica que posee tres lados, tres ángulos y tres vértices, teniendo como característica principal que uno de sus ángulos es recto. Esto quiere decir, que un ángulo interior de cada triángulo rectángulo mide exactamente 90° sexagesimales. Existen diferentes tipos de triángulos rectángulos, teniendo en cuenta sus lados y restantes ángulos interiores, pero siempre sin importar lo demás, uno de sus ángulos es recto.

Los triángulos en general, tienen unas características que permiten realizar cálculos, teniendo en cuenta todas ellas, y la principal es que la suma de los tres ángulos interiores de todos los triángulos es igual a 180° sexagesimales. Por lo que, podemos sacar de allí, dos cuestiones importantes acerca de los triángulos rectángulos.

Por un lado, podemos asegurar que la suma de los dos ángulos interiores que NO son el recto, es igual a 90° sexagesimales, es decir si la suma de a + b + c = 180° siendo c el ángulo recto, entonces a + b + 90° = 180° por lo tanto a + b = 90°.

A partir de esto, también podemos asegurar que los dos ángulos restantes, serán siempre agudos, ya que a + b = 90° significa que NINGUNO puede ser mayor a 90° y por lo tanto son agudos.

Las características de los triángulos rectángulo son:

• Tiene tres lados, tres vértices y tres aristas
• Uno de sus ángulos mide 90° sexagesimales
• Los dos ángulos que NO son rectos, son agudos
• La suma de los dos ángulos que NO son rectos, es igual a 90° sexagesimales
• Dos lados son perpendiculares y forman el ángulo de 90° sexagesimales.
• Son los polígonos que se utilizan para calcular el teorema de Pitágoras
• Tienen dos catetos y una hipotenusa
• La hipotenusa siempre es el lado de mayor longitud
• Con ellos se utilizan las razones trigonométricas

Vamos a darte algunos ejemplos de triángulos rectángulos que te permitirán entender mejor todo lo que te hemos contado.

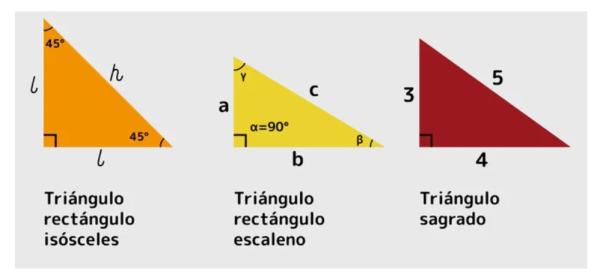
Triángulo 3-4-5

Este es uno de los ejemplos más conocidos y sencillos. Si un cateto mide 3 unidades y el otro mide 4 unidades, la hipotenusa medirá 5 unidades.

Triángulo Isósceles Rectángulo (o Triángulo 45-45-90)

En este tipo de triángulo, los dos catetos tienen la misma longitud. Los ángulos no rectos miden 45 grados cada uno.

Triángulo Rectángulo de Techos o Escaleras

Imagina una escalera apoyada contra una pared vertical en el suelo horizontal. La escalera, la pared y el suelo forman un triángulo rectángulo.

• La longitud de la escalera sería la hipotenusa.
• La altura que alcanza la escalera en la pared sería un cateto.
• La distancia desde la base de la pared hasta la base de la escalera en el suelo sería el otro cateto.

Triángulo Rectángulo en un Terreno o Mapa

Si trazas una línea recta hacia el este y luego una línea recta hacia el norte desde un punto de partida, y finalmente unes el punto final con el punto de partida, habrás formado un triángulo rectángulo.

• La línea que une el punto de partida y el punto final es la hipotenusa (la distancia en línea recta).
• Las distancias recorridas hacia el este y hacia el norte son los catetos.

Triángulo Rectángulo en la Geometría de un Monitor o Pantalla

La diagonal de un monitor de televisión o de una pantalla de teléfono se mide a menudo. Esta diagonal es la hipotenusa de un triángulo rectángulo cuyos catetos son el ancho y la altura de la pantalla.

Si un monitor tiene 16 pulgadas de ancho y 9 pulgadas de alto, la diagonal se calcularía usando el Teorema de Pitágoras.

Imagen: Enciclopedia Significados

Los triángulos rectángulos son polígonos de mucha importancia en matemática y geometría ya que son utilizados para cálculos de todo tipo como:

1. Geometría: estos triángulos se utilizan para construir y analizar otras figuras geométricas tales como prismas, rectángulos y cuadrados, entre otros.
2. Trigonometría: estos triángulos se utilizan para relacionar lados y ángulos usando las identidades trigonométricas como el seno, coseno y tangente. Con ello, se calculan distancias y medidas de ángulos faltantes.
3. Navegación y topografía: estos triángulos son utilizados históricamente para calcular la altura, la distancia y la posición.
4. Construcción: estos triángulos se utilizan para cálculos de diseños estructurales, medición de terrenos, construcción de edificios, puentes, etc.

Aquí te descubrimos qué es el teorema de Pitágoras con un vídeo hecho por uno de nuestros profesores:

Los triángulos rectángulos tienen diferentes usos, pero los más utilizados son mediante el teorema de Pitágoras y las razones trigonométricas.

Teorema de Pitágoras

El teorema de Pitágoras establece que “el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”. Esto quiere decir se escribe con una fórmula y es la siguiente:

hipotenusa² = cat. adyacente² + cat. opuesto²

En un triángulo rectángulo el lado que posee mayor longitud es la hipotenusa, que se encuentra opuesto al ángulo recto y los catetos son los lados que forman a este ángulo de 90° sexagesimales, siendo de menor longitud que la hipotenusa.

El teorema de Pitágoras puede utilizarse para calcular la medida de uno de sus lados cuando este es desconocido. Veamos algunos ejemplos.

Hipotenusa desconocida

Calcular el valor de la hipotenusa de un triángulo cuyos catetos miden 12 cm y 14 cm.

Utilizamos el teorema de Pitágoras teniendo como incógnita la hipotenusa, entonces:

• hipotenusa² = cat. adyacente² + cat. opuesto²
• hipotenusa² = 12² + 14²
• hipotenusa = raíz cuadrada (340)
• hipotenusa = 18,43

Por lo tanto la medida de la hipotenusa es 18,43 cm.

Cateto desconocido

Calcular el valor del cateto restante si la hipotenusa mide 20 cm y un cateto mide 16 cm.

Utilizamos el teorema de Pitágoras con uno de los catetos como incógnita, entonces:

hipotenusa² = cat. adyacente² + cat. opuesto²

• 20² = 16² + cateto²
• 400 - 256 = cateto²
• raíz cuadrada(144) = cateto
• 12 = cateto

Por lo tanto la medida del cateto faltante es igual a 12 cm.

A partir de estos ejemplos, podemos desglosar dos fórmulas a partir del teorema de Pitágoras y estas son:

• Cuando se desconoce la hipotenusa utilizamos la fórmula: hipotenusa = raíz cuadrada (cateto² + cateto²)
• Cuando se desconoce un cateto utilizamos la fórmula: cateto = raíz cuadrada (hipotenusa² - cateto²)

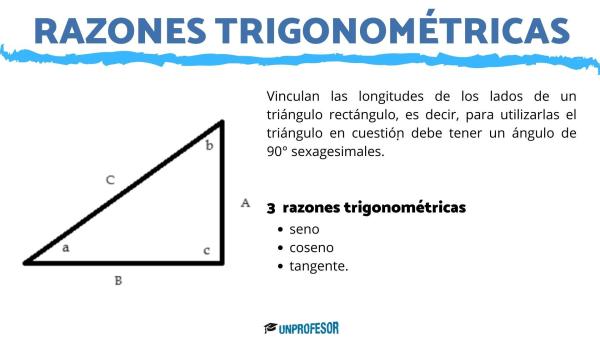
Razones trigonométricas

Las razones trigonométricas de los triángulos rectángulos relacionan los lados con los ángulos. Utilizamos en este caso nuevamente, los conceptos de hipotenusa y catetos, teniendo en cuenta que el cateto adyacente de un ángulo a, será el lado que lo forma, sabiendo que el otro es la hipotenusa, mientras que el lado opuesto, es el que se encuentra enfrente del mismo.

• Seno: el seno de un ángulo a es la relación que existe entre la hipotenusa y el cateto opuesto y su fórmula se escribe: sen a = cat. opuesto / hipotenusa
• Coseno: el coseno de un ángulo a es la relación que existe entre la hipotenusa y el cateto adyacente y su fórmula se escribe: cos a = cat. adyacente / hipotenusa
• Tangente: la tangente de un ángulo a es la relación que existe entre el cateto opuesto y el cateto adyacente y su fórmula se escribe: tng a = cat. opuesto / cat. adyacente

A partir de estas tres razones trigonométricas, que por cierto son las más importantes, se desprenden otras tres que son las siguientes:

• Cosecante: esta razón es la inversa al seno de un ángulo a, es decir, que la relación entre el cateto opuesto y la hipotenusa es al revés, siendo su fórmula: cosec a = hipotenusa / cat. opuesto
• Secante: esta razón es la inversa del coseno de un ángulo a, es decir, que la relación entre el cateto adyacente y la hipotenusa es al revés, siendo su fórmula: sec a = hipotenusa / cat. adyacente
• Cotangente: esta razón es la inversa de la tangente de un ángulo a, es decir, que la relación entre el cateto opuesto y el cateto adyacente es al revés, siendo su fórmula: cosec a = cat. adyacente / cat. opuesto

Si deseas leer más artículos parecidos a Qué es un triángulo rectángulo y ejemplos, te recomendamos que entres en nuestra categoría de Geometría.