Qué son los polígonos complejos y ejemplos

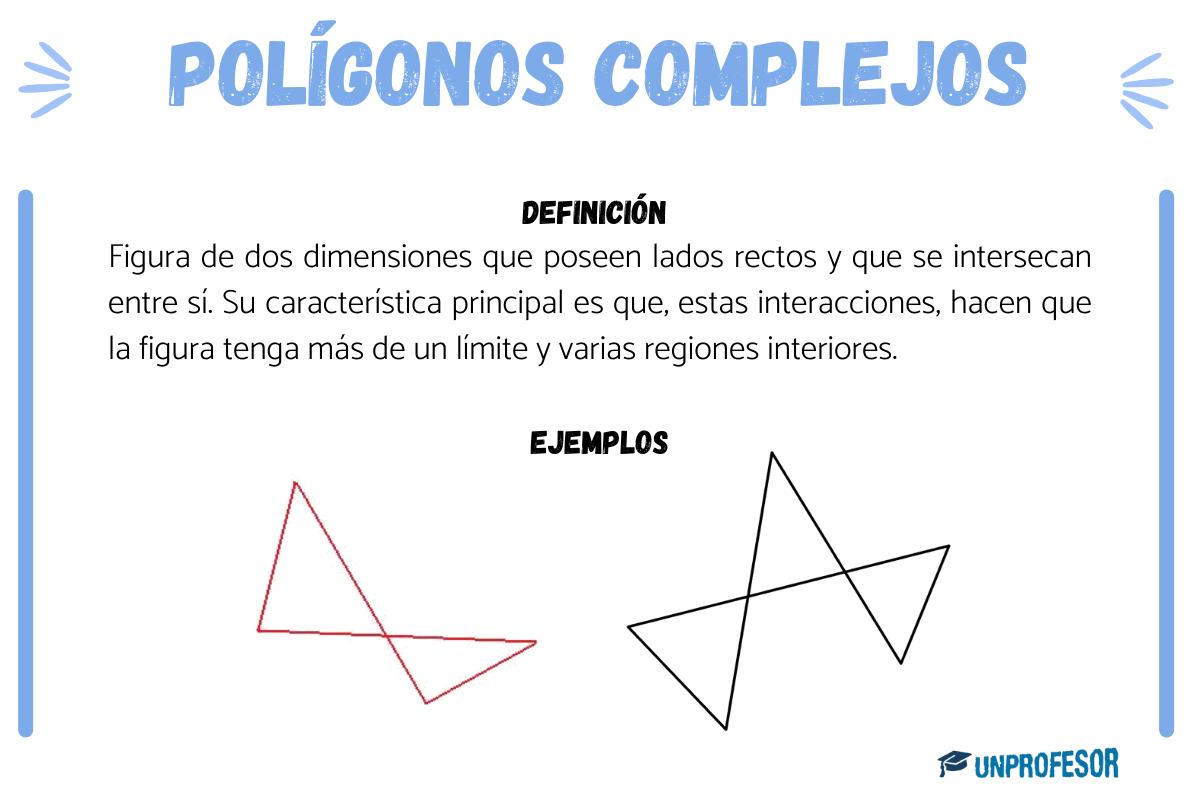
Un polígono complejo es una figura de dos dimensiones que poseen lados rectos y que se intersecan entre sí. Su característica principal es que, estas interacciones, hacen que la figura tenga más de un límite y varias regiones interiores. Estos polígonos también pueden llevar el nombre de polígonos cruzados debido a su característica principal.

La diferencia principal entre polígono simple y complejo es entonces, que los polígonos simples son figuras de dos dimensiones formadas por líneas rectas que NO se cruzan entre sí, mientras que los polígonos compuestos justamente están formados por líneas rectas que se cortan.

Podemos pensar a un polígono complejo como un elástico, cuyos lados pueden torcerse de forma tal que se crucen entre sí formando una figura compleja.

Los polígonos complejos pueden tener la forma de una estrella, y son conocidos como pentagramas, octagramas, hexagramas, etc.

Aquí te descubrimos los diferentes tipos de polígonos.

La estrella en sí misma no está definida en matemática, sin embargo se utiliza en polígonos, grafos y otros. A partir de polígonos simples y según algunos criterios pueden formarse polígonos estrellados diferentes.

Entonces bien, a partir de un polígono regular que tiene cantidad p de lados, se van a unir los vértices que sean no consecutivos de forma alternada, esto quiere decir que se va a marcar un orden de q vértices, hasta llegar al vértice inicial nuevamente formando así el polígono regular estrellado. Este polígono nuevo tendrá todos sus lados y ángulos iguales, es decir tendrán la misma medida. Ahora bien, representamos a la figura estrellada como {p/q}, expresión que se le atribuye a Ludwig Schläfli.

Ejemplos

Para entenderlo mejor, si tenemos un heptágono, la cantidad de lados será p=7, y queremos unir el primer vértice con el cuarto, esto significa que q=3. Debemos unir todos los vértices de tres en tres hasta llegar nuevamente al vértice inicial. El nuevo polígono estrellado será {7/3}.

Veamos un ejemplo más. Si queremos convertir un pentágono regular en un polígono regular estrellado, sabemos que tiene 5 lados que son iguales, por lo tanto p=5. Ahora bien, vamos a unir el primer vértice con el tercer vértice, por lo que q=2. Para poder continuar con el proceso, unimos el tercer vértice con el quinto vértice, el quinto vértice con el segundo vértice, el segundo vértice con el cuarto vértice, y para finalizar el cuarto vértice con el primer vértice. De esta manera obtenemos un polígono regular estrellado {5/2}.

Hay que tener en cuenta que un polígono estrellado debe tener la fracción que lo compone, es decir p/q irreducible, por lo tanto sus números deben ser primos relativos.

Para terminar de comprender esta lección, aquí te dejamos un repaso de los ejemplos de polígonos complejos.

Polígono regular estrellado {7/2}

Para realizar un polígono regular estrellado {7/2} debemos partir de un heptágono, por lo tanto p=7. Ahora bien, vamos a unir el primer vértice con el tercer vértice, ya que en el nombre del polígono estrellado, sabemos que q=2. Para continuar con el proceso, unimos el tercer vértice con el quinto vértice, el quinto vértice con el séptimo vértice, el séptimo vértice con el segundo vértice, el segundo vértice con el cuarto vértice, el cuarto vértice con el sexto vértice y para finalizar el sexto vértice con el primer vértice. De esta manera obtenemos un polígono regular estrellado {7/2}.

Como los valores de p y q son primos relativos, obtenemos un polígono estrellado regular {7/2}.

Polígono regular estrellado {8/3}

Otro de los ejemplos de polígonos complejos es un polígono regular estrellado {8/3}. Vamos a partir de un octógono. Esto quiere decir que p=8 y como vemos en su nombre sabemos también que q=3.

Ahora uniendo los vértices de tres en tres armamos nuestro polígono regular estrellado {8/3}. Unimos el primer vértice con el cuarto vértice, luego unimos el cuarto vértice con el séptimo vértice, el séptimo vértice con el segundo vértice, el segundo vértice con el quinto vértice, el quinto vértice con el octavo vértice, el octavo vértice con el tercer vértice, el tercer vértice con el sexto vértice y para finalizar el sexto vértice con el primer vértice. Así pues, obtenemos el polígono regular estrellado {8/3}.

Como bien mencionamos anteriormente, los polígonos estrellados regulares que vimos, tienen su fracción p/q irreducible. Pero, ¿qué pasa cuando la fracción NO lo es?

Esto significa que los vértices del polígono con el que iniciamos no quedaron todos unidos, y a partir de ellos se pueden obtener otros polígonos estrellados que permiten una especie de “segunda vuelta” siguiendo el mismo criterio utilizado antes. En vez de comenzar ahora por el primer vértice, se comienza por el “primer vértice NO conectado”, siguiendo luego las conexiones según sea q.

Esta nueva figura también puede generarse a partir de las superposición de dos polígonos estrellados girados. El ejemplo más conocido de estos polígonos es la Estrella de David, que se forma a partir de un hexágono con un orden de dos en dos, lo que sería un polígono regular estrellado {6/2}.

Si deseas leer más artículos parecidos a Qué son los polígonos complejos y ejemplos, te recomendamos que entres en nuestra categoría de Geometría.