Qué es una apotema y cómo se calcula


En una nueva lección de unProfesor estudiaremos qué es una apotema y cómo se calcula. En primer lugar vamos a repasar qué es un polígono. Después veremos la definición de apotema junto con sus características. Luego aprenderemos su fórmula y cómo se calcula, para terminar con algunos ejemplos.
¿Qué es la apotema?
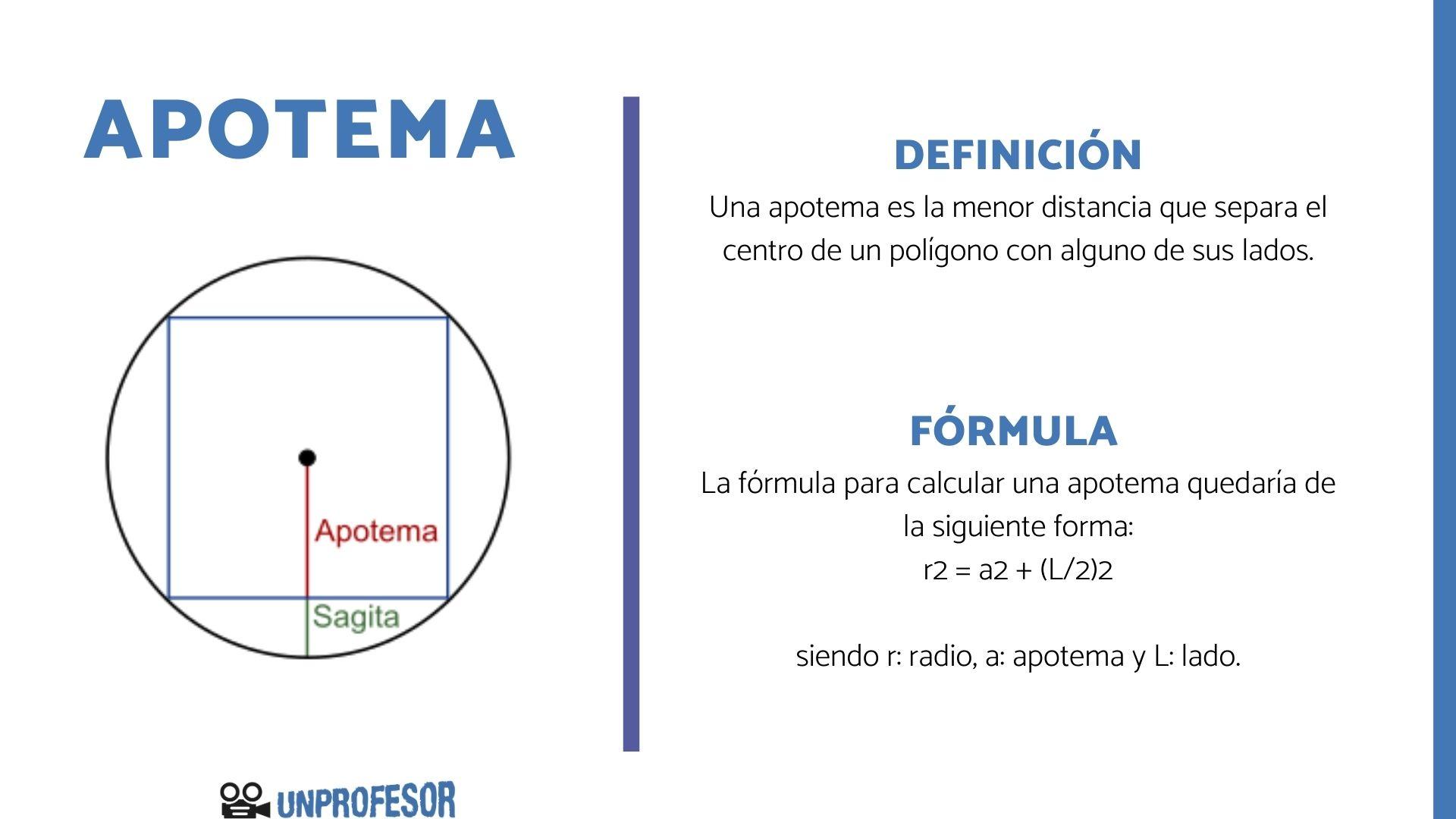
La apotema es la menor distancia que separa el centro de un polígono con alguno de sus lados. La apotema se representa mediante un segmento que une el centro de la figura con uno de sus lados. En el caso de los polígonos regulares, la apotema representa la distancia entre el centro y el medio de cualquiera de sus lados.
Dicho de otra forma, la apotema intersecta al lado de la figura en dos partes iguales, es decir divide al lado en dos.
La intersección entre la apotema y el lado de la figura regular forman cuatro ángulos de 90° sexagesimales, es decir que son perpendiculares y forman ángulos rectos.
Sagita
Si ubicamos un polígono regular circunscrito dentro de una circunferencia, la apotema será el segmento que une el centro de la circunferencia con otro punto de la misma, que pasa por el punto medio de un lado del polígono. La parte del segmento que une el medio del polígono con la circunferencia es lo que denominamos “sagita”.

¿Cómo se calcula una apotema?
Para calcular una apotema de los polígonos regulares, vamos a utilizar como referente al Teorema de Pitágoras.
Recordemos que el teorema de Pitágoras dice que en todo triángulo rectángulo, la suma de los cuadrados de las longitudes de sus catetos es igual al cuadrado de la longitud de la hipotenusa.
Entonces pensemos, que tenemos un polígono regular circunscrito dentro de una circunferencia. La apotema, el radio y la mitad del lado correspondiente a la misma, forman un triángulo rectángulo.
Entonces, la hipotenusa de mi triángulo será la medida correspondiente al radio, mientras que los catetos son, por un lado la mitad de la medida de uno de sus lados, y por el otro la apotema, cuyo valor desconocemos.
La fórmula para calcular la apotema quedaría de la siguiente forma:
r2 = a2 + (L/2)2
siendo r: radio, a: apotema y L: lado.
Despejamos la apotema, siendo esta la incógnita que queremos despejar de la ecuación.
r2 - (L/2)2 = a2
Raíz cuadrada(r2 - (L/2)2 )= a
De esta forma, podemos conocer el valor de la apotema de cualquier polígono regular.

Qué son los polígonos
En matemáticas, más específicamente en la rama de las geometrías, los polígonos son figuras geométricas del plano que se encuentran delimitadas por un número específico de líneas rectas.
Los polígonos están compuestos por lados, vértices, ángulos interiores, apotema y diagonales.
- Lados: segmentos rectos que forman la figura.
- Vértices: punto que une a dos lados que son consecutivos.
- Ángulos interiores: son los ángulos que se forman por dos lados que son consecutivos dentro de la figura.
- Apotema: línea recta que une el centro con los medios de los lados de la figura.
- Diagonales: son los segmentos de recta que unen a dos lados que no son consecutivos.
Los polígonos REGULARES son figuras geométricas con la particularidad de tener todos sus lados de la misma medida y sus ángulos interiores iguales.
Estas figuras pueden ser circunscritas dentro de una circunferencia. Dicho con otras palabras podemos contener una polígono regular dentro de una circunferencia que pasará por los vértices de la figura.
Tipos de polígonos regulares
Existen algunos tipos de polígonos regulares que se clasifican según la cantidad de lados que poseen.
- Cuadrado: cuadriláteros regulares con dos de sus lados opuestos paralelos y sus ángulos interiores rectos, es decir que mide 90° sexagesimales.
- Triángulo equilátero: Triángulos regulares con lados iguales y ángulos internos cada uno de 60° sexagesimales.
- Pentágono regular: es un polígono con 5 lados y ángulos internos que suman 180° sexagesimales.
- Hexágono regular: polígono con 6 lados de igual medida y ángulos internos que suman 120° sexagesimales.
- Heptágono regular: polígono con 7 lados iguales y ángulos interiores que suman 128,57° sexagesimales.
- Octágono regular: polígono con 8 lados iguales y ángulos interiores que suman 135° sexagesimales.
- Nonágono regular: polígono con 9 lados iguales.
En unProfesor te descubrimos los elementos de los polígonos regulares.
Ejemplo de cómo se calcula la apotema
Para aprender a calcular un apotema, aquí te dejamos 2 ejemplos fáciles de entender.
Ejemplo 1
Teniendo un polígono regular circunscrito en una circunferencia de radio 10 cm y lados 18 c, calcula la longitud de la apotema.
a= Raíz cuadrada(r2 - (L/2)2 )
Cambiamos los valores del radio y lado que nos ofrece como dato el ejercicio.
a= Raíz cuadrada(102 - (18/2)2 )
a= Raíz cuadrada(100 - 81)
a=Raíz cuadrada(19)
a=4,35
Es decir, la apotema mide 4,35 cm.
Ejemplo 2
Ahora tenemos un polígono regular de 6 cm de lado dentro de una circunferencia de radio 9 cm. ¿Cuál es el valor de la apotema?
Utilizamos la fórmula para calcularla.
a= Raíz cuadrada(r2 - (L/2)2 )
Ahora vamos a cambiar los valores del radio y lado que conocemos.
a=Raíz cuadrada(92 - (6/2)2 )
a= Raíz cuadrada(81 - 9)
a=Raíz cuadrada(72)
a=8,48
Entonces, el valor de la apotema es 8,48 cm.
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.
Si deseas leer más artículos parecidos a Qué es una apotema y cómo se calcula, te recomendamos que entres en nuestra categoría de Geometría.
- Pineda, C. E. G., & García, S. M. (2012). El área del paralelogramo y polígonos inscritos. Scientia et technica, 2(51), 161-165.
- Yanes, G. (2003). Acerca de la validez de la fórmula para calcular el área de un polígono regular.