Qué son los ángulos suplementarios - ejemplos


Los ángulos suplementarios son aquellos que sumados tienen una amplitud de 180° sexagesimales. En esta nueva lección de unProfesor estudiaremos qué son los ángulos suplementarios y ejemplos. Comenzaremos con la definición de ángulos suplementarios, continuaremos con algunos ejemplos y luego veremos cómo calcularlos. Para finalizar algunos ejercicios.
¿Qué son los ángulos suplementarios?
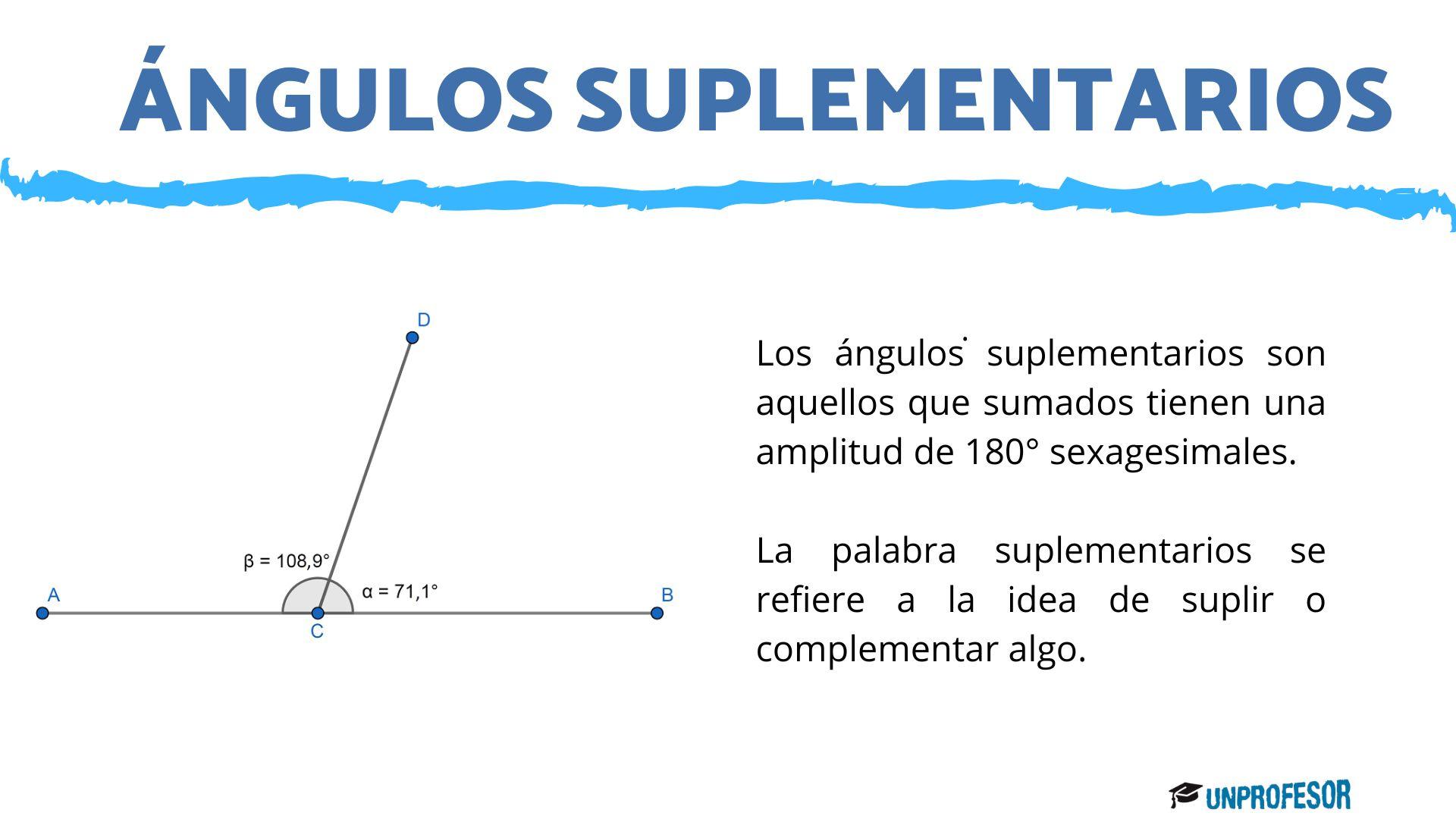
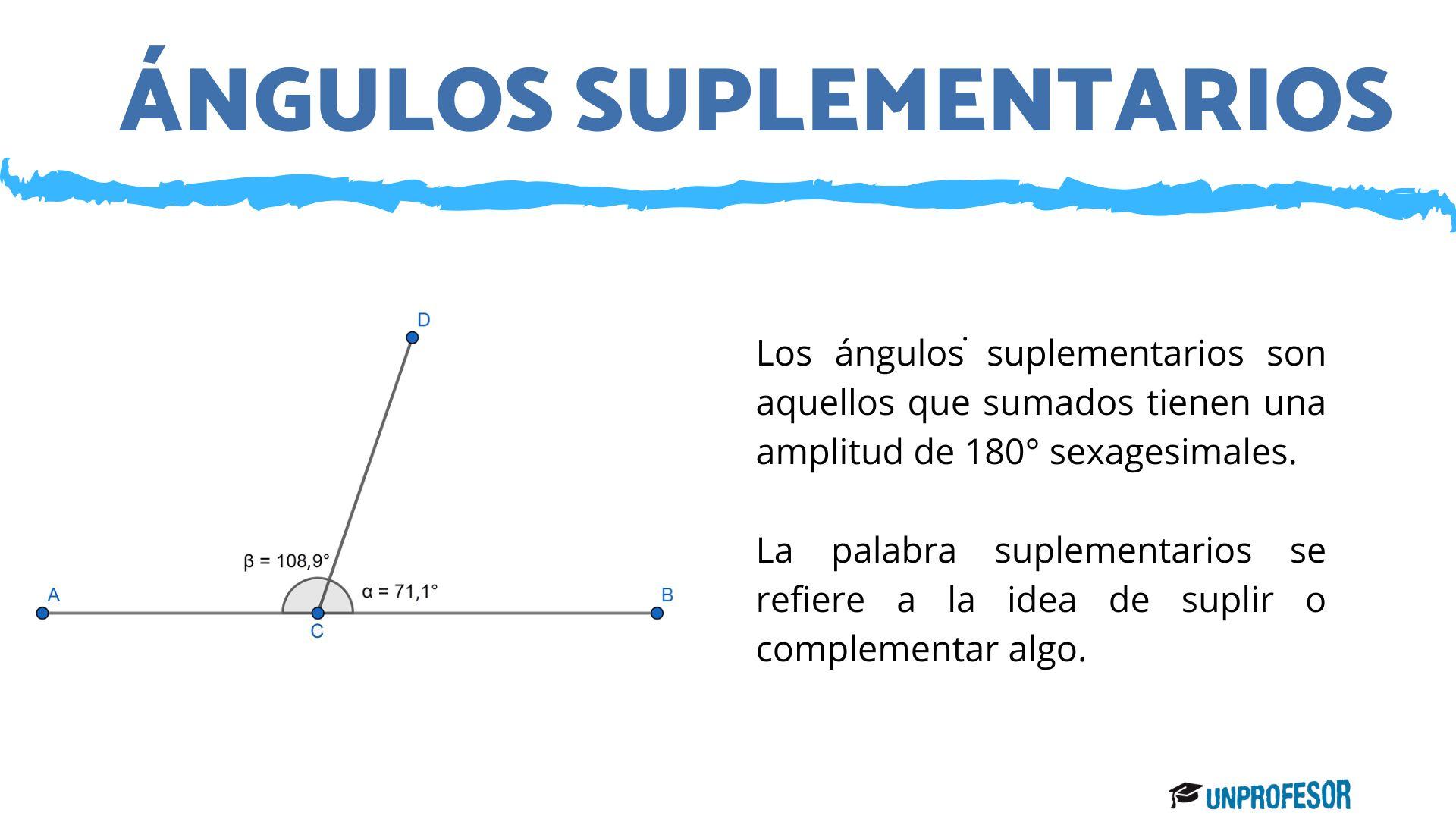
Según la posición de los ángulos, encontramos a los ángulos suplementarios que son aquellos que se forman cuando dos ángulos forman otro ángulo llano. Es decir, si la suma de dos ángulos es de 180° sexagesimales, entonces los ángulos son suplementarios.
La palabra suplementarios se refiere a la idea de suplir o complementar algo. Por lo tanto, los ángulos suplementarios, dan también como resultado dos ángulos rectos, es decir dos ángulos que miden 90° sexagesimales.
Recordemos que los ángulos son figuras que se forman a partir de dos semirrectas que se encuentran unidas por un punto, llamado vértice y que tienen una determinada amplitud, siendo esta, la distancia entre una semirrecta y la otra. Existen diferentes tipos y clasificaciones de ángulos. Por un lado, se dividen según su medida y por el otro según su posición.
Ejemplo
Por ejemplo, si tenemos dos ángulos suplementarios y uno mide 130° sexagesimales, el segundo mide entonces 50° sexagesimales.

Ejemplos de ángulos suplementarios
En la vida existen muchos ejemplos de estructuras que forman ángulos suplementarios y estas suelen ser de hecho, las que necesitan cargar o soportar demasiado peso.
Por ejemplo, se puede visualizar a los ángulos suplementarios en algunos puentes con arcos, carpas que se utilizan para eventos grandes como cumpleaños o casamientos y las vigas que sostienen casas que se colocan perpendiculares al suelo, entre otros.
Veamos ejemplos de ángulos suplementarios más concretos con algunos números.
- Si dos ángulos son suplementarios y uno mide 75°, el otro medirá 105° sexagesimales.
- Si dos ángulos son suplementarios y uno de ellos mide 46°, el otro medirá 134° sexagesimales.
- Si un ángulo mide 210° sexagesimales, entonces no tendrá un ángulo suplementario ya que posee una medida mayor a 180° sexagesimales solo.
- Un ángulo que mide 52° y otro que mide 25° no podrán ser suplementarios ya que la suma de ambos es menor a 180° sexagesimales.

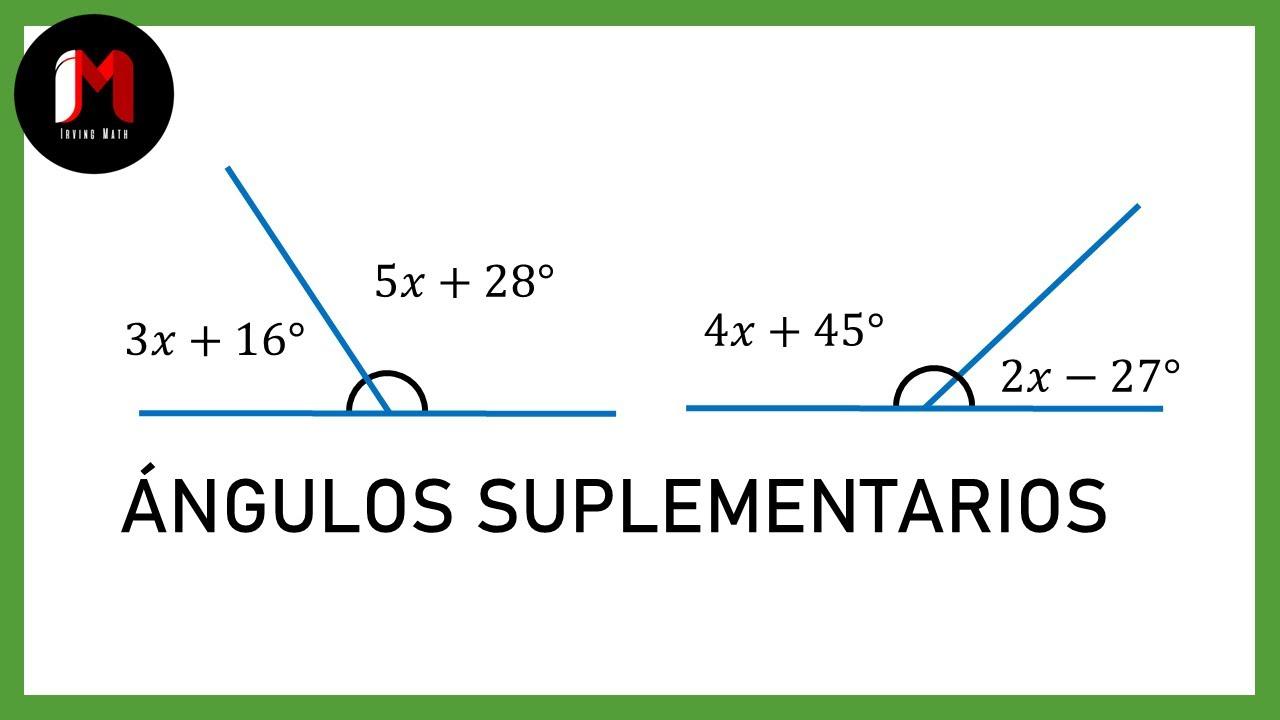
Cómo calcular los ángulos suplementarios
Para saber cuánto mide un ángulo que es suplementario a otro debemos calcular la diferencia entre la suma, que debe ser igual a 180°, y el ángulo que conocemos.
Por ejemplo, si tenemos un ángulo que mide 89° y es suplementario a otro x, debemos realizar la diferencia entre el total, que es 180° y 89°, para encontrar el valor de x, entonces:
- x = 180° - 89°
- x = 91°
Entonces el ángulo x que suplementa a 89° sexagesimales tiene una apertura de 91° sexagesimales.
Otro ejemplo, queremos encontrar la medida del ángulo b siendo este suplementario a un ángulo de 146° sexagesimales. Calculamos:
- b = 180° - 146°
- b = 34°
Entonces el ángulo b que suplementa a 146° sexagesimales tiene una apertura de 34° sexagesimales.

Ejercicios con ángulos suplementarios
Aquí encontrarás algunos ejercicios con ángulos suplementarios que te ayudarán a comprender y apropiarte del concepto de ángulos suplementarios.
1- ¿Los siguientes ángulos son suplementarios o no? Justifica tu respuesta.
- 45° y 89°
- 122° y 58°
- 175° y 23°
- 62° y 118°
- 133° y 47°
- 230° y 12°
- 15° y 165°
- 43° y 26°
- 95° y 85°
2- Calcular cuánto mide el ángulo suplementario faltante.
- 29° y a
- 78° y b
- 126° y c
- 173° y d
- 125° y e
- 144° y f
- 88° y g
Soluciones
Ejercicio 1:
- 45° y 89° no son suplementarios, ya que 45° + 89° = 134° y no suman 180°.
- 122° y 58° son suplementarios, ya que 122° + 58° = 180°.
- 175° y 23° no son suplementarios, ya que 175° + 23° = 198° y supera los 180°.
- 62° y 118° son suplementarios, ya que 62° + 118° = 180°.
- 133° y 47° son suplementarios, ya que 133° + 47° = 180°.
- 230° y 12° no son suplementarios, ya que solo el primer ángulo supera los 180°.
- 15° y 165° son suplementarios, ya que 15° + 165° = 180°.
- 43° y 26° no son suplementarios, ya que 43° + 26° = 69° y no suman 180°.
- 95° y 85° son suplementarios, ya que 95° + 85° = 180°.
Ejercicio 2:
- 29° y a. Calculamos la diferencia: a = 180° - 29° = 151°. Entonces a mide 151° sexagesimales.
- 78° y b. Calculamos la diferencia: b = 180° - 78° = 102°. Entonces b mide 102° sexagesimales.
- 126° y c. Calculamos la diferencia: c = 180° - 126° = 54°. Entonces c mide 54° sexagesimales.
- 173° y d. Calculamos la diferencia: d = 180° - 173° = 7°. Entonces d mide 7° sexagesimales.
- 125° y e. Calculamos la diferencia: e = 180° - 125° = 55°. Entonces e mide 55° sexagesimales.
- 144° y f. Calculamos la diferencia: f = 180° - 144° = 36°. Entonces f mide 36° sexagesimales.
- 88° y g. Calculamos la diferencia: g = 180° - 88° = 92°. Entonces g mide 92° sexagesimales.
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.
Si deseas leer más artículos parecidos a Qué son los ángulos suplementarios - ejemplos, te recomendamos que entres en nuestra categoría de Geometría.