Qué son los ángulos congruentes - ejemplos


Dos ángulos son congruentes si tienen la misma medida. En la nueva lección de unProfesor que te presentamos hoy, hablaremos de qué son los ángulos congruentes y ejemplos. Comenzaremos con la definición de congruencia de ángulos, continuaremos con algunos ejemplos y terminaremos con ejercicios sobre el tema para que puedas apropiarte del concepto.
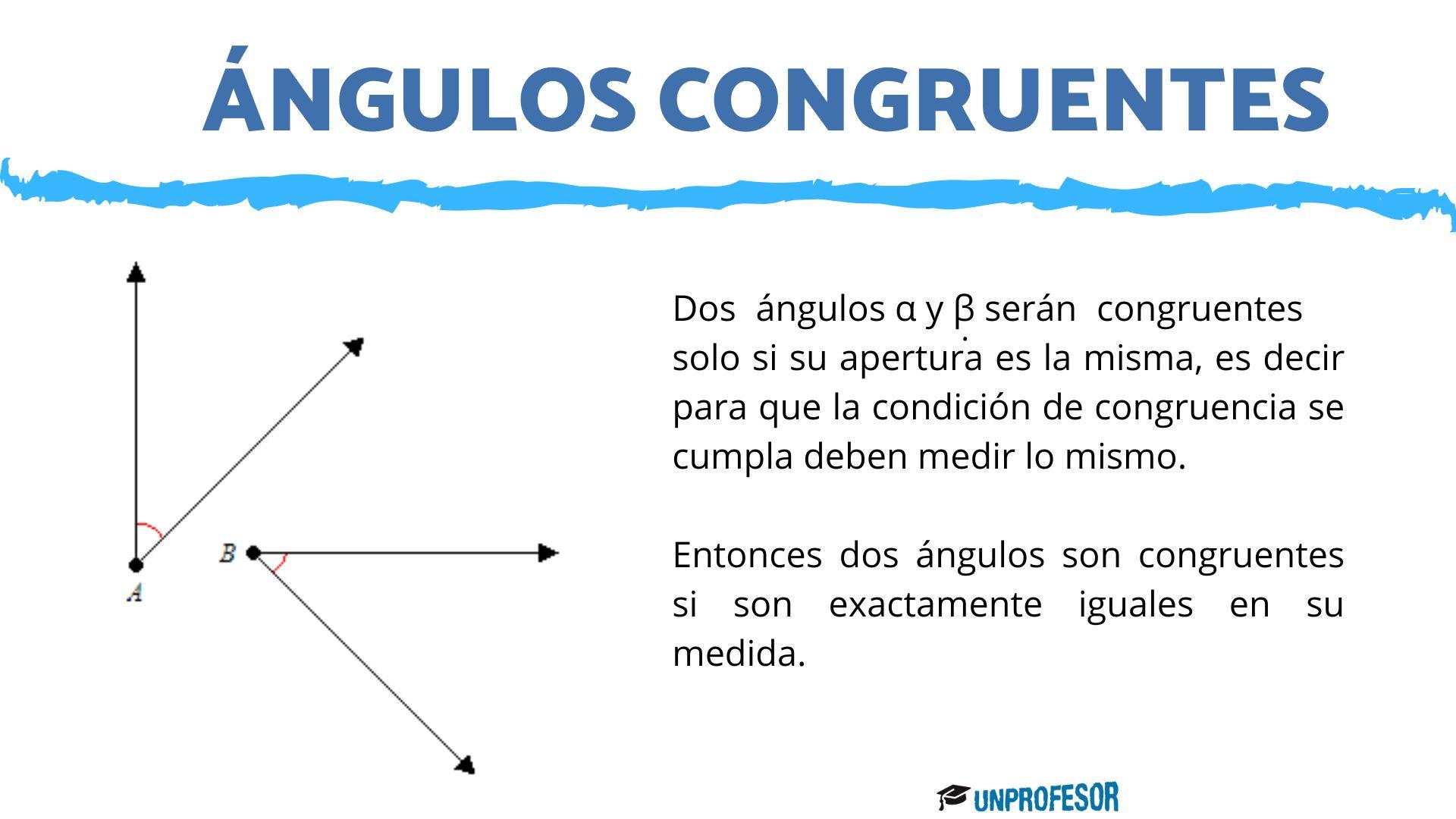
¿Qué son los ángulos congruentes?
Dos ángulos α y β serán congruentes solo si su apertura es la misma, es decir para que la condición de congruencia se cumpla deben medir lo mismo. Entonces dos ángulos son congruentes si son exactamente iguales en su medida.
Este concepto se utiliza mucho en matemáticas, sobre todo en geometría para clasificar o definir la congruencia entre figuras geométricas, por ejemplo, para saber si dos triángulos son congruentes, entonces comparamos que sus ángulos interiores sean congruentes.
Si α mide 60° sexagesimales, entonces β debe medir 60° sexagesimales para que sean congruentes. Si α mide 45° sexagesimales y β tiene otra medida de apertura, entonces podemos asegurar que NO son congruentes.
Para que dos ángulos sean congruentes no tienen que estar apuntando en la misma dirección y tampoco tienen que estar formados por dos semirrectas que miden lo mismo, sino que es la apertura entre el vértice y esas dos semirrectas la que indica si tienen o no la misma medida, y por lo tanto si son o no congruentes.

Ejemplos de ángulos congruentes
Aquí te dejamos diferentes ejemplos de ángulos congruentes:
- Ángulos opuestos por el vértice: los ángulos que se encuentran entre dos semirrectas que se cruzan son cuatro. Los dos pares de ángulos que se encuentran opuestos por el vértice son congruentes entre sí, ya que tienen la misma medida de apertura. Es decir, si nombramos a los ángulos a, b, c y d, en sentido de las agujas de un reloj, podremos asegurar que a y c son congruentes, así como b y d.
- Ángulos alternos: cuando una recta cualquiera, corta dos rectas paralelas forma ángulos alternos internos y alternos externos. Esos ángulos que se forman son congruentes entre sí, es decir en este ejemplo, tendremos cuatro pares de ángulos congruentes.
- Triángulos equiláteros: como estos triángulos tienen la particularidad de que todos sus lados son iguales, los ángulos que se forman también son todos iguales, por lo tanto los triángulos equiláteros tienen tres ángulos congruentes y miden 60° sexagesimales.
- Triángulos isósceles: la particularidad de estos triángulos es que tienen dos lados iguales, por lo que tienen también dos ángulos iguales. Estos mismos son congruentes.
- Cuadrado: los cuadrados poseen la particularidad de que todos sus lados son iguales, y aparte de ello tienen cuatro ángulos que miden 90° sexagesimales, por lo que serán todos congruentes.
- Rectángulo: los rectángulos tienen dos pares de lados iguales, pero los ángulos son todos rectos, de la misma forma que en un cuadrado, por lo que sus cuatro ángulos son congruentes.
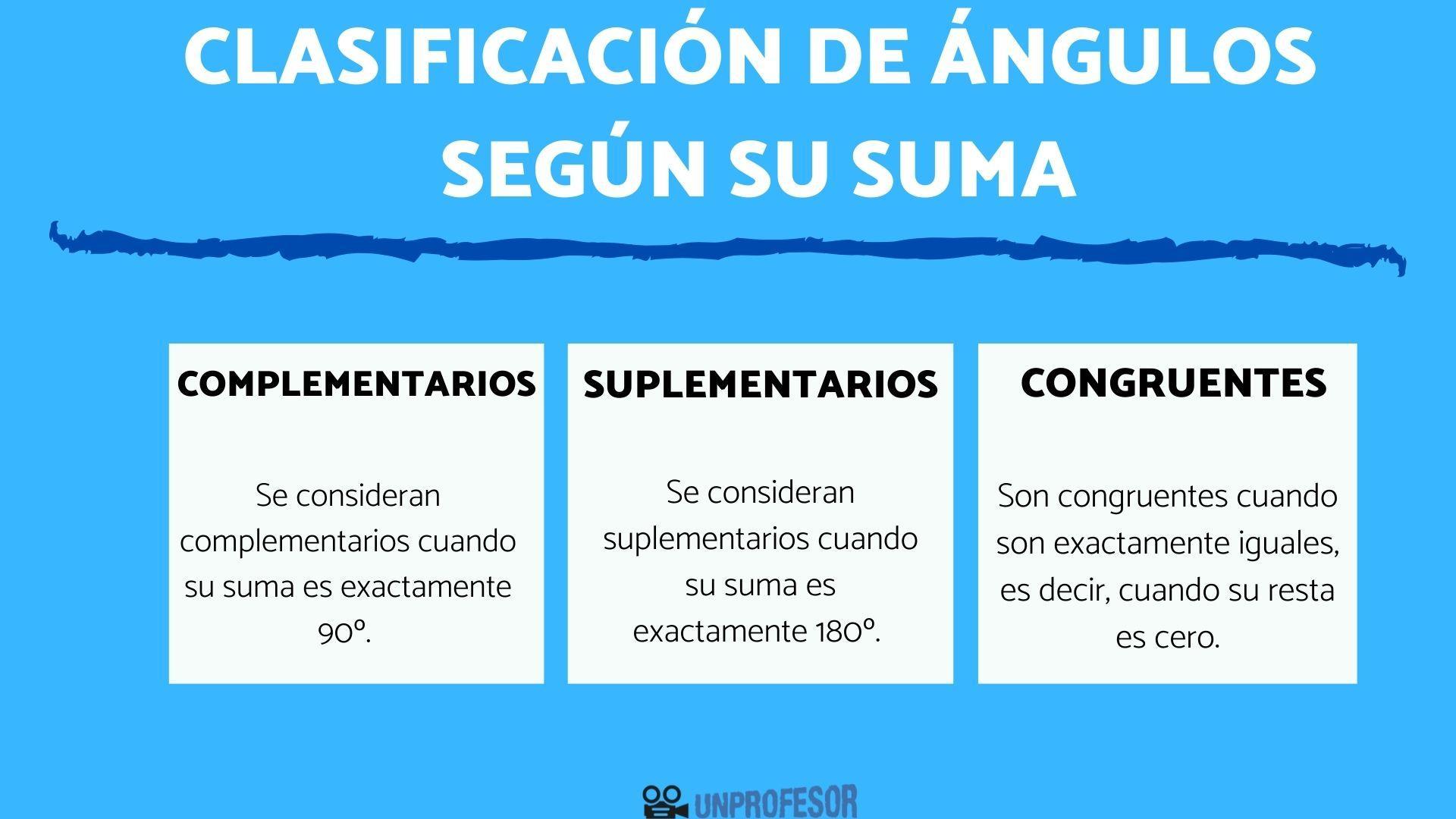
Descubre aquí la clasificación de los ángulos según su suma:

Ejercicios con ángulos congruentes
Aquí te dejamos diferentes ejercicios con ángulos congruentes y sus soluciones para que puedas practicar en casa.
1) Completar la oración:
- Un ángulo α mide 75° sexagesimales y su congruente β mide ……..
- Un triángulo isósceles posee un ángulo de 88°, otro de 46° y su congruente de ……
- Un triángulo con tres ángulos congruentes es un triángulo ……..
- Un ángulo que mide 89° sexagesimales tiene un congruente que mide …..
- Si dos pares de ángulos congruentes miden 65° y 115° son …………
2) Decir si las siguientes afirmaciones son Verdadero o falso.
- Un ángulo recto posee dos ángulos congruentes si es cortado por su bisectriz
- Los cuadrados solo poseen dos ángulos congruentes
- Los rectángulos tienen cuatro ángulos congruentes
- Los ángulos que se forman cuando una recta corta dos paralelas son todos congruentes
- Los ángulos de un triángulo isósceles son todos congruentes
- Los ángulos de un triángulo equilátero son todos congruentes
- Dos ángulos llanos son congruentes
- Dos ángulos agudos son congruentes
Soluciones
Ejercicio 1:
- Un ángulo α mide 75° sexagesimales y su congruente β mide 75° sexagesimales.
- Un triángulo isósceles posee un ángulo de 88°, otro de 46° y su congruente de 46° sexagesimales.
- Un triángulo con tres ángulos congruentes es un triángulo equilátero.
- Un ángulo que mide 89° sexagesimales tiene un congruente que mide 89° sexagesimales.
- Si dos pares de ángulos congruentes miden 65° y 115° son opuestos por el vértice.
Ejercicio 2:
- Verdadero. Un ángulo recto mide 90° sexagesimales, y con su bisectriz se forman dos ángulos de 45° sexagesimales, por lo tanto los ángulos son congruentes.
- Falso. Los cuadrados tienen cuatro ángulos congruentes que miden 90° sexagesimales.
- Verdadero. Los rectángulos tienen cuatro ángulos congruentes que miden 90° sexagesimales.
- Falso. Los ángulos que se forman cuando una recta corta dos paralelas no son todos congruentes, sino que existen dos pares que sí lo son.
- Falso. Los ángulos de un triángulo isósceles son dos congruentes mientras que el tercero no lo es.
- Verdadero. Los ángulos de un triángulo equilátero son todos congruentes y miden 60° sexagesimales.
- Verdadero. Dos ángulos llanos son congruentes y miden 180° sexagesimales.
- Falso. Dos ángulos agudos son congruentes si y sólo sí miden lo mismo, pero no necesariamente los ángulos agudos serán iguales.
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Qué son los ángulos congruentes - ejemplos, te recomendamos que entres en nuestra categoría de Geometría.