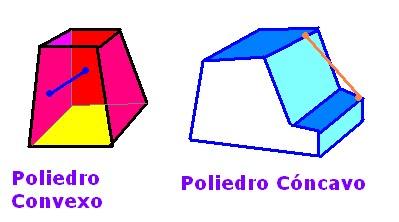
Diferencias entre poliedros cóncavos y convexos - ejemplos


En esta ocasión, desde unProfesor vamos a explicarte cuáles son las diferencias entre los poliedros cóncavos y convexos, lección muy importante y básica para el estudio de las matemáticas y, en concreto, de geometría. En primer lugar, aclararemos conceptos: qué es un poliedro y qué significa que sea cóncavo o convexo. Después, daremos paso a los ejemplos. Por último, propondremos un ejercicio y su solución para comprobar que se ha entendido la explicación.
Qué es un poliedro
Los poliedros son cuerpos geométricos que tienen un número determinado de caras planas que son polígonos. Son figuras tridimensionales y han de ser acotados, es decir, limitados por un número determinado y finito de superficies planas. O sea, no puede ser un poliedro aquella figura que tiene infinitas caras.
Por lo tanto, encierran un volumen finito. Pueden ser de distintos tipos, pero en este artículo vamos a diferenciar entre los cóncavos y los convexos.

Cuáles son las diferencias entre poliedros cóncavos y convexos
- Cóncavo: Que un poliedro sea cóncavo significa que si cogemos dos puntos cualesquiera del poliedro podemos encontrar un segmento de recta que sobresalga del poliedro al exterior. Por ejemplo, pensemos en un poliedro que tenga forma de zigzag en tres dimensiones, si uniéramos una de las puntas superiores con la siguiente, estaríamos trazando un segmento que iría por fuera del poliedro y, por lo tanto, es cóncavo.
- Convexo: Por otro lado, que un poliedro sea convexo quiere decir que si cogemos dos puntos cualesquiera del poliedro, la línea que les une es interna a la figura, o sea, el segmento no sobresale al exterior del poliedro. Los poliedros convexos cumplen que el número de caras más el número de vértices menos el número de aristas es 2. Si pensamos en una caja de zapatos, cojamos los puntos que cojamos de ese poliedro, si los unimos siempre vamos a trazar un segmento que pasará por dentro de la caja.

Ejemplos de poliedros cóncavos y convexos
- Como ejemplos de poliedros cóncavos, encontramos el toroide facetado, que tiene forma de donut, una figura de escalones, una flecha en tres dimensiones, un zigzag... En definitiva, cualquier forma aleatoria que tenga algún tipo de hendidura o agujero. En el día a día vemos poliedros cóncavos, por ejemplo las gomas del pelo o las escaleras.
- Como ejemplo de poliedros convexos, encontramos todos aquellos que son regulares, como el tetraedro, el cubo o hexaedro regular, el dodecaedro, el icosaedro y el octaedro. También otras figuras como el prisma rectangular o la pirámide cuadrangular. Si pensamos en la vida cotidiana, podemos considerar poliedros convexos las cajas de cartón, una tabla de madera...

Ejercicios de poliedros cóncavos y convexos
Es hora de practicar con los siguientes ejercicios:
1. Justifica si las oraciones que leerás a continuación son ciertas o falsas:
- Los poliedros regulares son siempre convexos.
- Los poliedros cóncavos siempre tienen hendiduras o agujeros.
- Los poliedros pueden englobar un volumen infinito dependiendo de si son cóncavos o convexos.
- La convexidad implica que el poliedro sea regular.
2. Elabora un dibujo de un poliedro convexo y otro de un poliedro cóncavo y comprueba que en el primero todos los segmentos pasan por el interior, pero que en el segundo alguno pasa por el exterior.
Solución
Las soluciones a los ejercicios anteriores son las siguientes:
1.
- Los poliedros regulares son siempre convexos: cierto, porque los poliedros regulares son el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro y los cinco son regulares.
- Los poliedros cóncavos siempre tienen hendiduras o agujeros: cierto, para que al unir dos puntos del poliedro el segmento esté en el exterior.
- Los poliedros pueden englobar un volumen infinito dependiendo de si son cóncavos o convexos: falso, ya que los poliedros siempre engloban un volumen finito, nunca infinito.
- La convexidad implica que el poliedro sea regular: falso, un poliedro puede ser convexo pero no regular, como por ejemplo una caja de zapatos, porque es convexo, pero no se incluye en ninguno de los cinco poliedros regulares ya mencionados.
2. Dependiendo del dibujo elaborado, la respuesta puede variar. Respuesta abierta.
Si este artículo te ha parecido útil, no dudes en navegar por la pestaña de Matemáticas o utilizar el buscador en la parte superior de la web. ¡Podrás encontrar más información sobre los poliedros! También puedes compartirlo con tus compañeros de clase.
Si deseas leer más artículos parecidos a Diferencias entre poliedros cóncavos y convexos - ejemplos, te recomendamos que entres en nuestra categoría de Geometría.