Tipos de triángulos y sus ángulos


En esta nueva publicación de unPROFESOR te traemos un tema sumamente importante en matemáticas y, más específicamente, en el área de geometría: los tipos de triángulos y sus ángulos. Para abordar este tema comenzaremos por explicar qué es un triángulo de manera teórica y cuál es su relación con los ángulos que estos poseen. Posteriormente, expondremos los tipos de triángulos que existen basándonos en los ángulos que los forman. Asimismo, para potenciar el proceso de aprendizaje, facilitaremos imágenes de estos triángulos para que la explicación sea más gráfica.
- Definición de triángulo
- Los ángulos de los triángulos
- ¿Cómo se clasifican los triángulos según sus ángulos?
- Tipos de triángulos según sus ángulos
- Ángulo de un triángulo escaleno
- Ángulo de un triángulo isósceles
- Ángulo de un triángulo equilátero
- Ángulo de un triángulo acutángulo
- Clasificación de triángulos según sus ángulos: ejercicios
Definición de triángulo
En geometría, nos referimos a un triángulo cuando se trata de un polígono que resulta de unir tres puntos diferentes con líneas rectas; y en consecuencia, se forma una figura geométrica que cuenta con tres lados (a, by c), tres vértices (A, B y C) y tres ángulos que se encuentran en el interior de la figura geométrica. Es más, el propio nombre de la figura ya sugiere su misma composición, “triángulo”: evidencia que el número tres es esencial para la comprensión geométrica y matemática del polígono en cuestión.
En el siguiente apartado profundizaremos en la relación que existe entre los ángulos que conforman esta figura y su calificación basada en estos.

Los ángulos de los triángulos
Los triángulos, como se puede intuir por su nombre, tienen siempre tres ángulos. Estos ángulos siempre suman 180º, sin importar de qué tipo de triángulo estemos hablando.
No obstante, los ángulos más comunes son los agudos, ya que los triángulos solo pueden tener, como mucho, un ángulo recto o un ángulo obtuso, nunca más de uno.
Si hablamos de la clasificación de los triángulos según sus ángulos, podemos encontrarnos tres tipos de triángulos: l
- Los obtusángulos
- Los rectángulos
- Los acutángulos

¿Cómo se clasifican los triángulos según sus ángulos?
Además de lo mencionado en el apartado anterior, para entender los triángulos es fundamental comprender la relación que existe con los ángulos que lo conforman. Por tal motivo, es esencial mencionar que todo triángulo, independientemente de su nombre o clasificación, está compuesto por tres ángulos, los cuales sumados siempre darán un total de 180 grados. Es decir, no importa a que triangulo sea haga referencia incluso si este está clasificado según sus lados, en cualquier caso la suma de los ángulos de un triángulo siempre será 180.
En este sentido, otro elemento importante es que un triángulo no puede tener más de un ángulo recto (90 grados) u obtuso (mayor de 90 grados).
Visto este concepto y vínculo fundamental entre el triángulo y sus ángulos, vamos a proceder a mencionar los tipos de triángulos que existen según la medida de sus ángulos internos.

Tipos de triángulos según sus ángulos
Antes de presentar los tipos de triángulos según sus ángulos, desde unPROFESOR consideremos importante señalar que si bien existen otros tipos de triángulos, estos son con base a sus lados.
Dicho esto, continuemos con el tema central de esta lección. Los tipos de triángulos y sus ángulos se dividen en dos: triángulo rectángulo y triángulo oblicuángulo; este último, con una subdivisión: acutángulo y obtusángulo.
Triángulo rectángulo
Son triángulos que tienen un ángulo recto (de 90 grados). En este caso, y para profundizar en la teoría, el lado opuesto a este ángulo de 90, tiene el nombre de hipotenusa y los otros dos lados se le llama catetos. Hay que tener en cuenta, que la hipotenusa siempre será mayor que los catetos de este triángulo. Asimismo, en un triángulo rectángulo los dos ángulos agudos (menores de 90 grados) son complementarios y su suma siempre debe dar en 90 grados.
Triángulos acutángulos
Son triángulos que están formados por tres ángulos agudos; es decir, todos sus ángulos miden menos de 90 grados.
Triángulos obtusángulos
Como su nombre lo indica, son triángulos que tienen un ángulo obtuso; es decir, mayor de 90 grados.

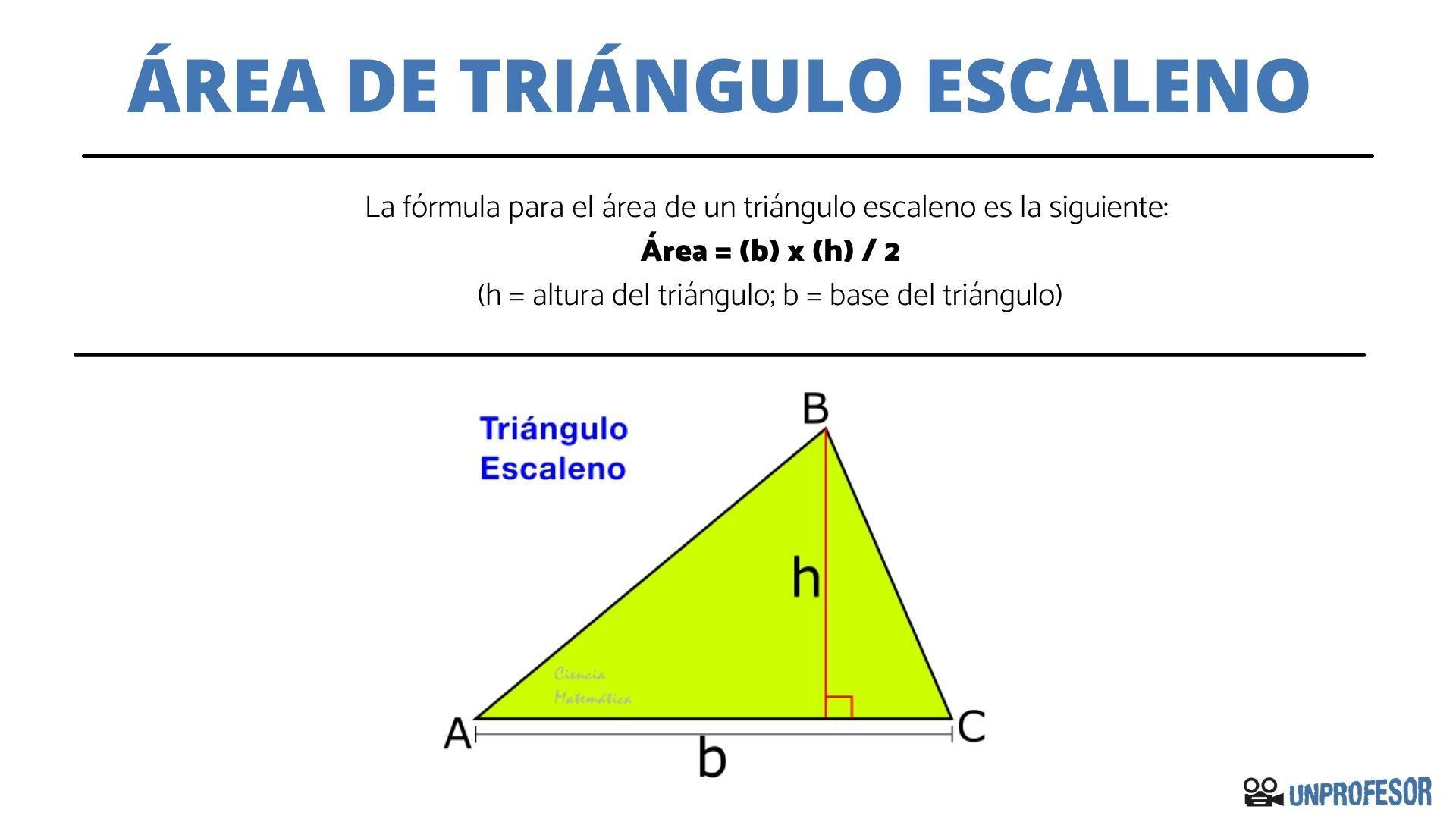
Ángulo de un triángulo escaleno
Un triángulo escaleno, como ya sabemos por otras lecciones de unProfesor, es aquel que tiene todos los lados de distinta longitud, lo cual implica que todos sus ángulos serán distintos.
En este tipo de triángulo, uno de los ángulos es recto u obtuso, mientras que los otros dos son agudos. Es decir, encontramos un ángulo de 90º o más, pero los otros dos son menores a 90º.
Entonces, básicamente podemos encontrar dos tipos:
- Triángulo escaleno rectángulo: un ángulo mide 90º y los otros dos son agudos.
- Triángulo escaleno obtusángulo: un ángulo mide más de 90º y los otros dos son agudos.

Ángulo de un triángulo isósceles
Un triángulo isósceles es aquel que tiene dos lados exactamente iguales en longitud, mientras que el otro es distinto. De este modo, en un triángulo isósceles siempre encontraremos dos ángulos que tendrán la misma amplitud y un tercero con distinta amplitud.
Los triángulos isósceles pueden ser:
- Triángulo isósceles acutángulo: la totalidad de sus ángulos son agudos, es decir, menores a 90º.
- Triángulo isósceles rectángulo: tiene un ángulo recto, o sea, de 90º, mientras que los otros dos son agudos y miden exactamente 45º.
- Triángulo isósceles obtusángulo: el ángulo que se encuentra en la unión de los dos lados que son iguales es obtuso, mientras que los otros dos son agudos.

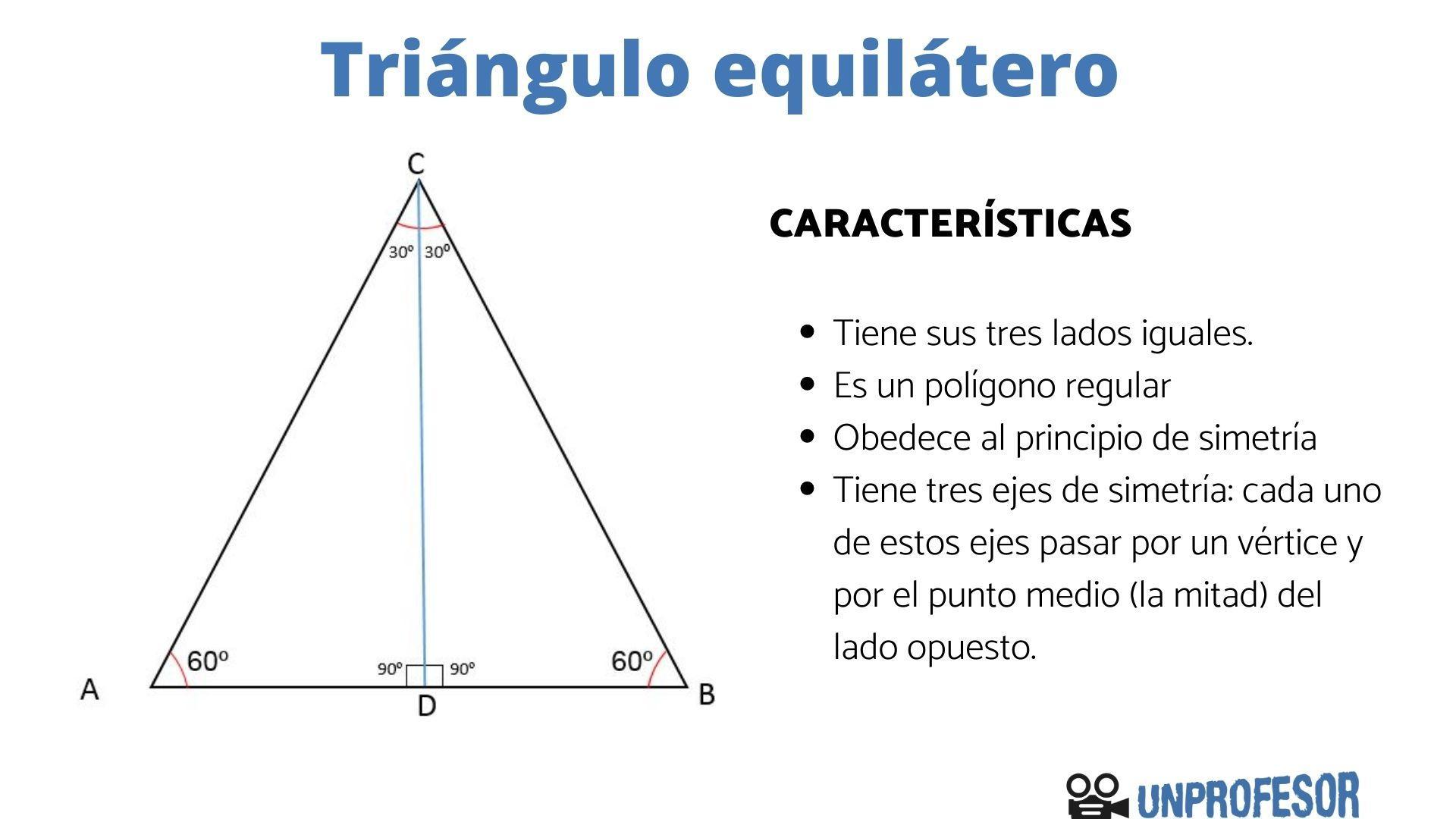
Ángulo de un triángulo equilátero
Un triángulo equilátero es aquel que tiene sus tres lados iguales y, por lo tanto, tiene también sus tres ángulos iguales. Por ello, solo hay un tipo de ángulo que podemos encontrar en este tipo de triángulo: el ángulo de 60º.
Recordemos que todos los triángulos tienen la propiedad de que sus ángulos deben sumar 180º y de que, además, tienen siempre 3 ángulos. Entonces, si sabemos que los triángulos equiláteros tienen los 3 ángulos iguales, solo tenemos que dividir 180 entre 3 y nos da 60. En definitiva, sus tres ángulos son agudos.

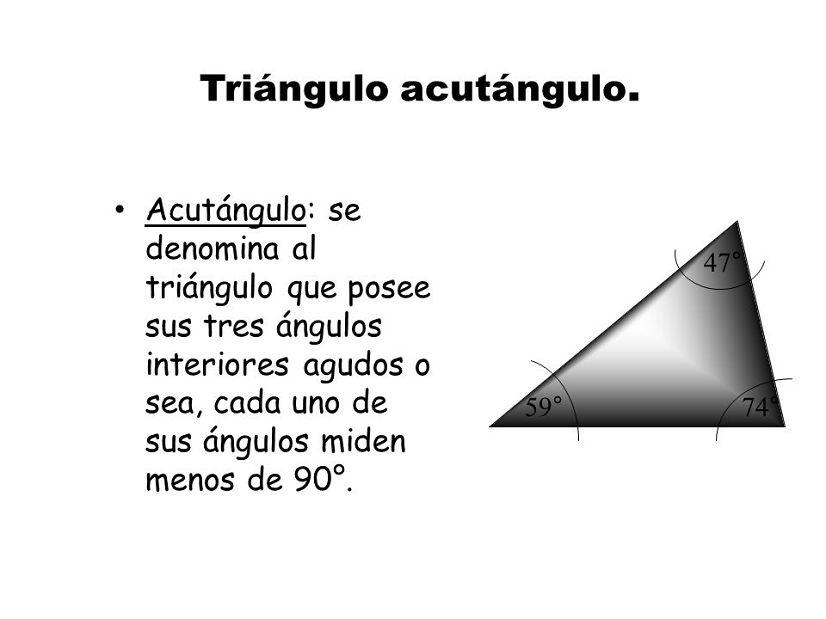
Ángulo de un triángulo acutángulo
Un triángulo acutángulo tiene sus tres ángulos agudos, es decir, los tres ángulos miden menos de 90º. Es una manera de clasificar los triángulos según sus ángulos, por lo que es compatible con la clasificación por lados de los triángulos.
Es decir, podemos considerar que un triángulo equilátero es acutángulo o que un triángulo isósceles es acutángulo.

Clasificación de triángulos según sus ángulos: ejercicios
Para que puedas poner en práctica lo que se ha explicado en esta lección, te recomendamos que realices los ejercicios que te proponemos a continuación:
1. Decide y justifica si las siguientes oraciones son verdaderas o falsas:
- Un triángulo acutángulo siempre será equilátero.
- Un triángulo equilátero siempre será acutángulo.
- Los triángulos escalenos no pueden ser acutángulos.
- Los triángulos rectángulos siempre tienen un ángulo de 90º.
Soluciones
Vamos a verificar si has hecho correctamente las actividades planteadas:
1. Decide y justifica si las siguientes oraciones son verdaderas o falsas:
- Un triángulo acutángulo siempre será equilátero: no, un triángulo puede tener sus tres ángulos agudos de diferentes medidas, no hace falta que sean todos iguales.
- Un triángulo equilátero siempre será acutángulo: sí, ya que los triángulos equiláteros tienen siempre sus ángulos de 60º, lo cual los convierte en agudos.
- Los triángulos escalenos no pueden ser acutángulos: verdadero, ya que por lo menos uno de sus ángulos debe ser recto u obtuso.
- Los triángulos rectángulos siempre tienen un ángulo de 90º: verdadero, es una condición necesaria para que se considere triángulo rectángulo.
Si deseas leer más artículos parecidos a Tipos de triángulos y sus ángulos, te recomendamos que entres en nuestra categoría de Geometría.
- Quishpe Vaca, J. M. (2018). Estudio de los triángulos (Master's thesis, Universidad Nacional de Educación).
- Llantén, V. H. (2009). Construcción de triángulos.
- Verdugo, A. C. (2016). Clasificación de triángulos de acuerdo a la longitud de sus lados: una propuesta para la enseñanza y aprendizaje en geometría. Revista Boletín Redipe, 5(4), 42-49.