Cuáles son las aristas de un triángulo

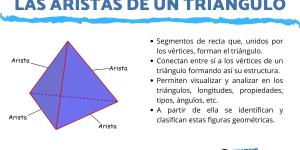
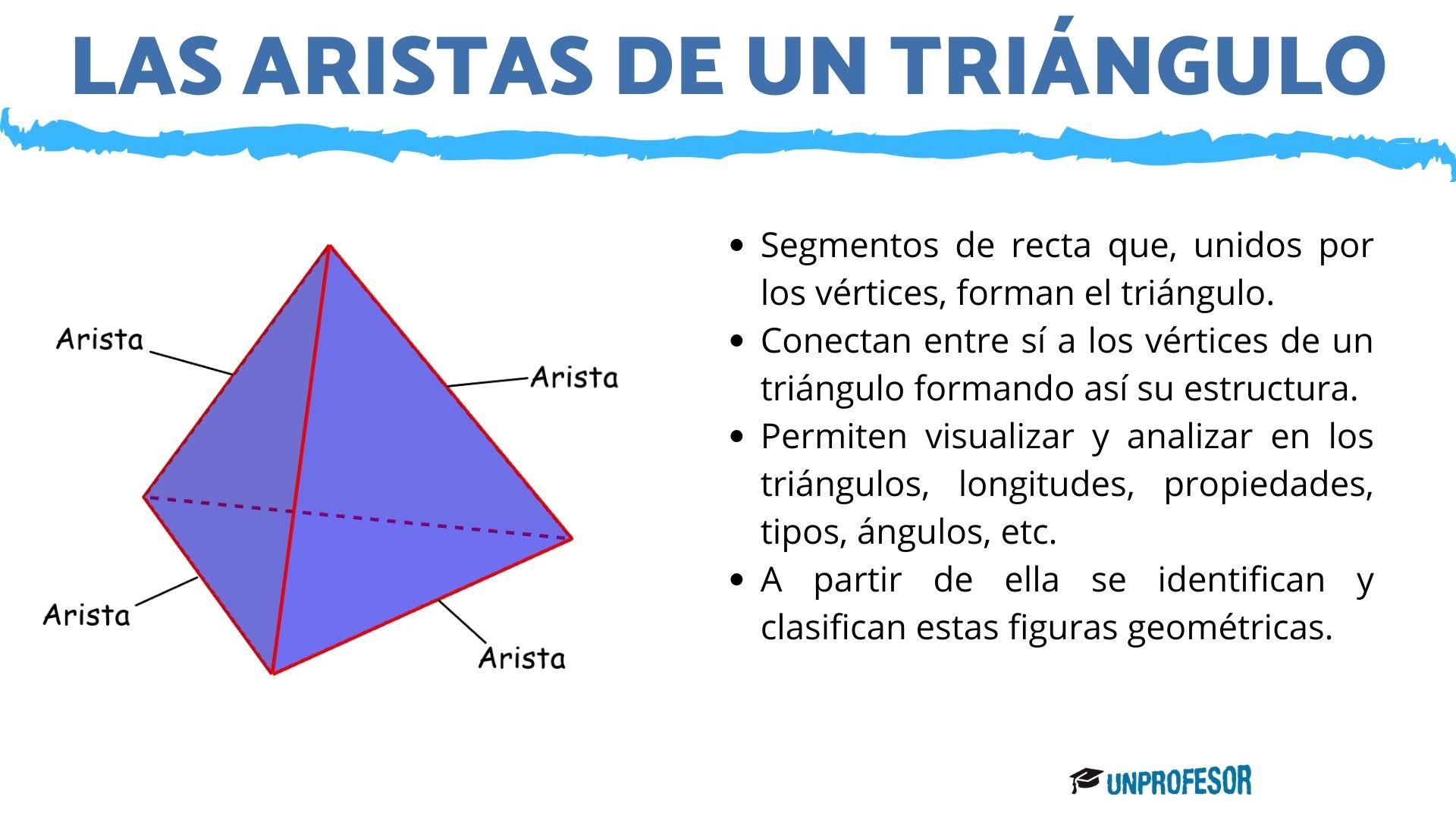
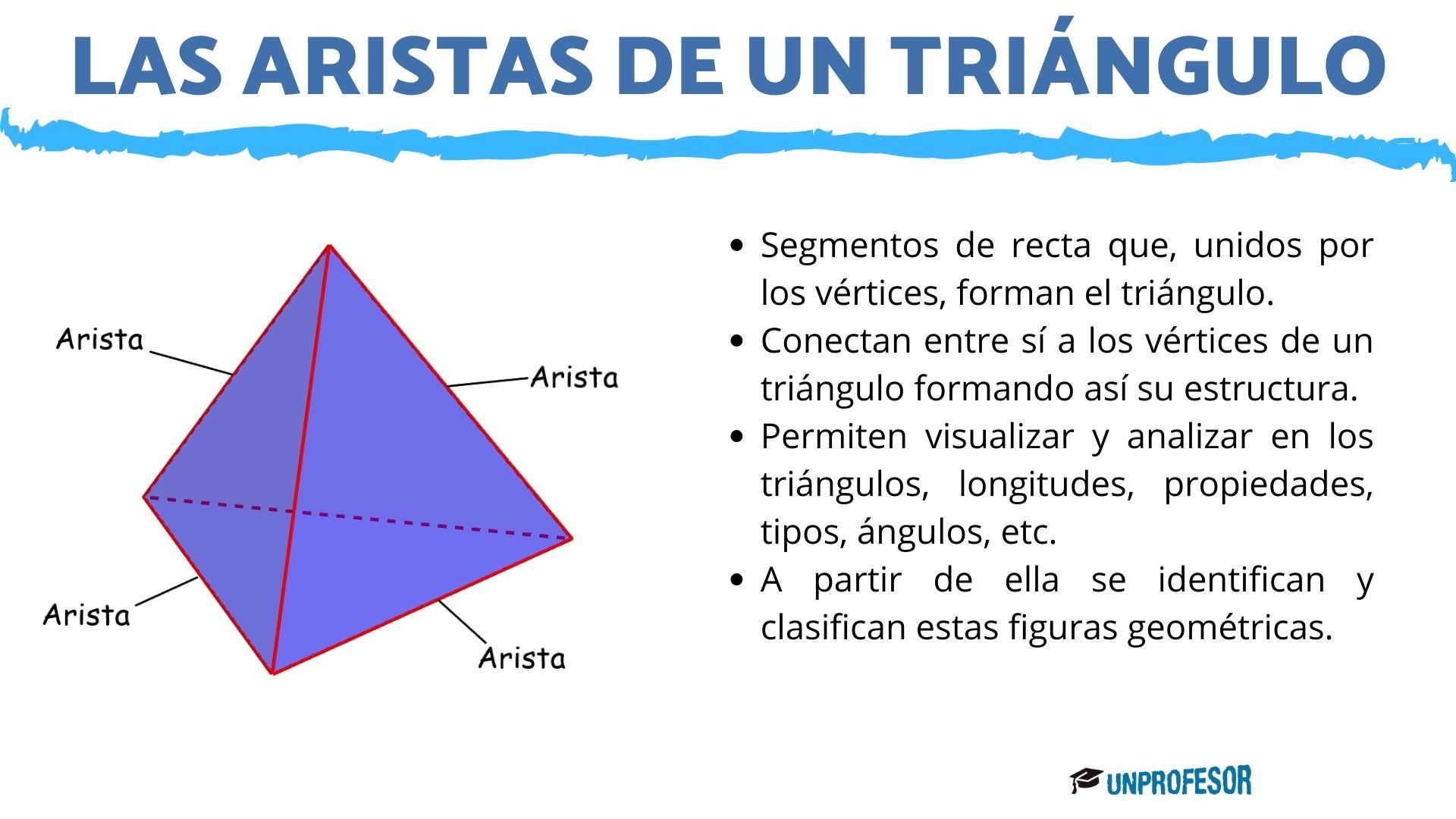
Las aristas de un triángulo son los segmentos de recta que unidos por los vértices forman el triángulo. Estas aristas son las que conectan entre sí a los vértices de un triángulo formando así su estructura. Cada una de ellas, establece una relación entre dos vértices, que van a ser los puntos donde finaliza la semirrecta, y formando una distancia o longitud específica en esa figura. Las aristas son las líneas que permiten visualizar y analizar en los triángulos, longitudes, propiedades, tipos, ángulos, etc.

Las aristas son muy importantes debido a que a partir de ella se identifican y clasifican estas figuras geométricas. Se comparan las longitudes de sus medidas y los ángulos que lo forman, y a partir de allí se determinan las características que poseen, el perímetro, área, entre otras.

En matemáticas, las aristas y ángulos son fundamentales para utilizar las razones trigonométricas y el teorema de Pitágoras.

Ahora que ya sabes cuáles son las aristas de un triángulo, vamos a conocer qué son estos elementos. Los triángulos son las figuras geométricas más básicas de la geometría. Son polígonos planos que se forman por tres aristas, tres vértices y tres ángulos.

La suma de los ángulos interiores de un triángulo siempre es igual a 180° sexagesimales. Y uno de los teoremas más importantes o más utilizados en matemáticas es el teorema de Pitágoras, que se realiza a partir de un triángulo rectángulo.

Existen diferentes tipos de triángulos según las aristas o los ángulos interiores que lo forman.

Elementos de un triángulo

Los elementos de un triángulo son:

• Vértices: son puntos en donde las aristas se encuentran, es decir el punto donde se unen los lados de un triángulo. Existen tres vértices en cada uno. Los vértices junto con los lados, forman los ángulos interiores de cada triángulo.
• Ángulos: es la apertura que se forma a partir de dos aristas que se unen en uno de los vértices. Cada triángulo posee siempre tres ángulos interiores. También existen tres ángulos exteriores en cada uno, debido a la apertura exterior entre un vértice y dos lados.
• Aristas: son los lados que forman el triángulo, y también siempre serán tres.

Según la longitud de sus aristas, existen tres tipos de triángulos:

• Equiláteros: los triángulos equiláteros son aquellos cuyas aristas miden exactamente lo mismo las tres. Es decir, todos los lados del triángulo tienen la misma medida.
• Isósceles: los triángulos isósceles son aquellos que poseen dos aristas con la misma medida, mientras que la tercera tiene otra longitud. Es decir, dos lados son iguales y uno diferente.
• Escaleno: los triángulos escalenos son aquellos cuyas tres aristas tienen medidas diferentes, es decir sus tres lados poseen longitudes diferentes.

El teorema de Pitágoras es un apartado que relaciona los lados de un triángulo rectángulo. Para poder utilizarlo, siempre debemos contar con un ángulo recto, de lo contrario el teorema no puede utilizarse.

Este mismo, relaciona las longitudes de dos de los lados de un triángulo con su hipotenusa, veamos que dice:

“el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma del cuadrado de los catetos”

La hipotenusa de un triángulo rectángulo es la arista que se encuentra opuesta al ángulo recto, mientras que los catetos son las dos aristas que forman este ángulo.

La fórmula del teorema de Pitágoras es la siguiente:

H² = A² + B²

Siendo H la hipotenusa, y A y B los catetos.

Ejemplo del Teorema de Pitágoras

Cómo se utiliza: por ejemplo, tenemos un triángulo rectángulo cuyos catetos miden A = 4 cm y B = 6 cm. ¿Cuánto mide la arista faltante del mismo?

Para saber la medida de la arista faltante, debemos hallar la hipotenusa, ya que conocemos las medidas de los catetos. Entonces utilizamos la fórmula:

• H² = A² + B²
• H² = 4² + 6²
• H² = 16 + 36despejamos el cuadrado de la incógnita
• H = raíz (52)
• H = 7,21 cm
• La medida de la arista faltante es 7,21 cm.

Las razones trigonométricas son fórmulas que se utilizan para relacionar un ángulo con dos aristas de un triángulo rectángulo. Las principales o básicas son: el seno, el coseno y la tangente. Veamos sus fórmulas:

• Seno: el seno de un ángulo “x” es igual a la razón entre el cateto opuesto y la hipotenusa. sen x = Cat. Opuesto / Hipotenusa
• Coseno: el coseno de un ángulo “x” es igual a la razón entre el cateto adyacente y la hipotenusa. cos x = Cat. Adyacente / Hipotenusa
• Tangente: la tangente de una ángulo “x” es igual a la razón entre el cateto opuesto y el cateto adyacente. tg x = Cat. Opuesto / Cat. Adyacente

Las razones que se utilizan dependen del valor faltante que necesitamos descubrir y los datos que nos proporciona el ejercicio, es decir, debemos conocer dos valores para hallar el tercero. Los ángulos “x” son los dos ángulos que no son rectos, y dependiendo de ellos cuáles serán los catetos, es decir su opuesto y adyacente varían según cuál sea.

Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.

Si deseas leer más artículos parecidos a Cuáles son las aristas de un triángulo, te recomendamos que entres en nuestra categoría de Geometría.