Área de un polígono regular


En esta lección de unProfesor os explicaremos cómo hallar el área de un polígono regular. Para ello, antes necesitamos saber qué es un polígono regular. Un polígono regular es aquel que todos sus lados son iguales y todos sus ángulos son iguales. En esta lección te ofrecemos la fórmula, con ejemplos y ejercicios resueltos para que puedas practicar en casa.
Qué es un polígono regular
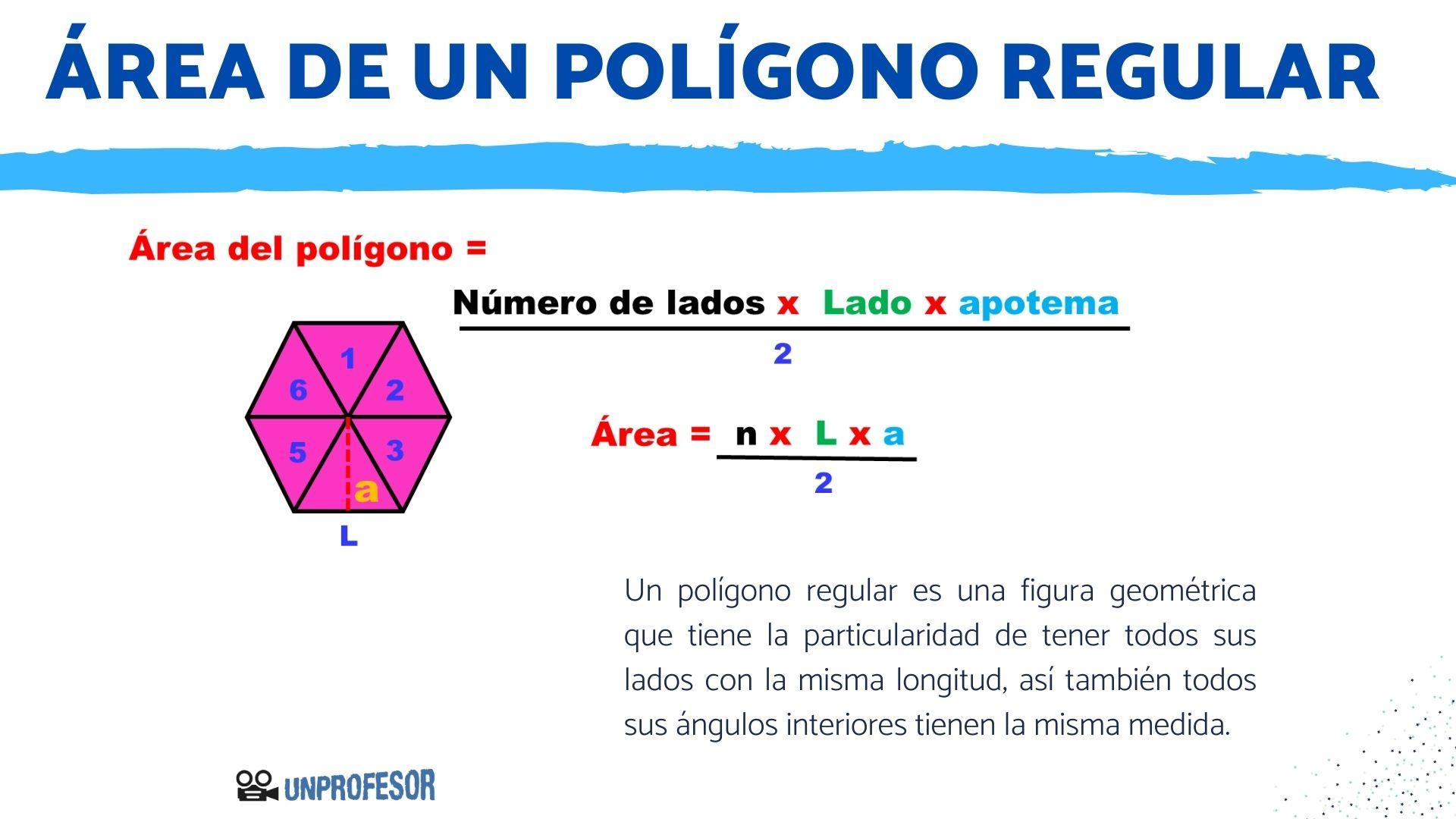
Un polígono regular es una figura geométrica que tiene la particularidad de tener todos sus lados con la misma longitud, así también todos sus ángulos interiores tienen la misma medida.
Los polígonos regulares son equiláteros y equiangulares. Son figuras geométricas en el plano que están constituidas por segmentos de recta que son no colineales y que forman un espacio cerrado. Estos polígonos pueden ser circunscritos en una circunferencia, es decir pueden estar contenidos dentro de una circunferencia que pasa por todos los vértices del polígono regular.
A parte, los polígonos pueden contener a su vez una circunferencia que sea tangente a tus lados, es decir una circunferencia inscrita en el polígono regular.

Cómo calcular el área de un polígono regular: fórmula
Para calcular el área de un polígono regular necesitamos conocer el perímetro de un polígono regular.
Perímetro (P)
Equivale a multiplicar el número de lados por la longitud de los lados.
P = n x L
Fórmula para calcular el área de un polígono regular
Una vez conocido el perímetro, la fórmula del área de un polígono regular es la multiplicación entre el perímetro y el apotema, y luego se divide por 2.
También podemos expresar el área en términos diferentes, ya que a veces no conocemos el valor de la apotema.
Ejemplo
Calcular el perímetro y área de un polígono regular de seis lados, donde cada lado mide 12 metros.
Primero calculamos el perímetro. Tenemos n = 6 y L = 12 m.
Entonces:
P = n x L = 6 x 12 m = 72 m
Ahora bien, podemos calcular el área de la figura.

Elementos de un polígono regular
Los elementos de un polígono regular son:
- Vértices: Puntos cuya unión forman los lados de la figura geométrica. El número de vértices coincide con el número de lados de la figura.
- Lados: Son los segmentos de recta que unen los vértices formando así el polígono.
- Ángulos internos: Es el arco que se forma de la unión de los lados de la figura.
- Apotema: Es la línea perpendicular que une el centro del polígono con el punto medio de alguno de sus lados.
- Diagonales: Son aquellos segmentos de recta que unen cada uno de los vértices con sus vértices opuestos.

Tipos de polígonos regulares
Vamos a conocer los tipos de polígonos regulares según el número de lados que lo componen
- Triángulo equilátero: triángulo regular con lados idénticos y sus ángulos internos miden 60º
- Cuadrado: cuadrilátero regular, específicamente, un paralelogramo. Sus dos lados opuestos son paralelos entre sí. Sus ángulos interiores son rectos y miden 90º.
- Pentágono regular: es un polígono que posee cinco caras. Sus ángulos interiores miden 108º.
- Hexágono regular: Es un polígono que tiene seis lados de la misma longitud y sus ángulos internos suman 120º.
- Heptágono regular: Es un polígono regular de siete lados con sus ángulos interiores de 128,57º.
- Octógono regular: Es un figura que posee ocho lados de la misma medida y sus ángulos interiores miden 135º.
- Nonágono regular: Es un polígono regular que tiene nueve lados.

Ejercicios para hallar el área de un polígono regular (con soluciones)
Ejercicio 1
Calcular el perímetro y área de un polígono regular de 5 lados cuyo lado mide 8 cm y la apotema 5.5 cm.
Solución
P = n x L =5 x 8 cm = 40 cm
A = P x a2 = 40 cm x 5.5 cm2 = 220 cm22 = 110 cm2
El perímetro del polígono regular es de 40 cm y el área es de 110cm2
Ejercicio 2
Calcular el perímetro y área de un polígono regular de 6 lados de 10 cm cada uno.
Solución
P = n x L = 6 x 10 cm = 60 cm
A = n x L24 x tan(180°n) = 6 x 1024 x tan(180°6) = 6002.3094 = 259.80 cm2
El perímetro del polígono regular es de 60 cm y el área es de 259.80cm2
Ejercicio 3
Calcular el perímetro y área de un polígono regular de 8 lados cuyo lado mide 6 cm y la apotema 3.5 cm.
Solución
P = n x L =8 x 6 cm = 48 cm
A = P x a2 = 48 cm x 3.5 cm2 = 168 cm22 = 84 cm2
El perímetro del polígono regular es de 48 cm y el área es de 84cm2
Ejercicio 4
Calcular el perímetro y área de un polígono regular de 9 lados de 7 cm cada uno.
Solución
P = n x L = 9 x 7 cm = 63 cm
A = n x L24 x tan(180°n) = 9 x 724 x tan(180°9) = 4411.455 = 303 cm2
El perímetro del polígono regular es de 63 cm y el área es de 303cm2

Si deseas leer más artículos parecidos a Área de un polígono regular, te recomendamos que entres en nuestra categoría de Geometría.