Cómo calcular el área de un octaedro


Para calcular el área de un octaedro debemos hacer la suma de las superficies de las ocho caras que posee. En unProfesor te descubrimos la fórmula y ejemplos para que lo entiendas mejor. Un octaedro es una figura geométrica tridimensional que está formada por ocho polígonos. Es un poliedro que puede ser regular o irregular pero que siempre posee ocho caras que pueden ser iguales o no. Dependiendo de esto, se puede o no calcular el área de un octaedro.
En una nueva lección de unProfesor vamos a trabajar cómo calcular el área de un octaedro. Comenzaremos con el concepto de octaedro, luego seguiremos con los elementos que componen el octaedro. Continuaremos con el cálculo del área para finalizar con algunos ejercicios.
¿Qué es un octaedro?
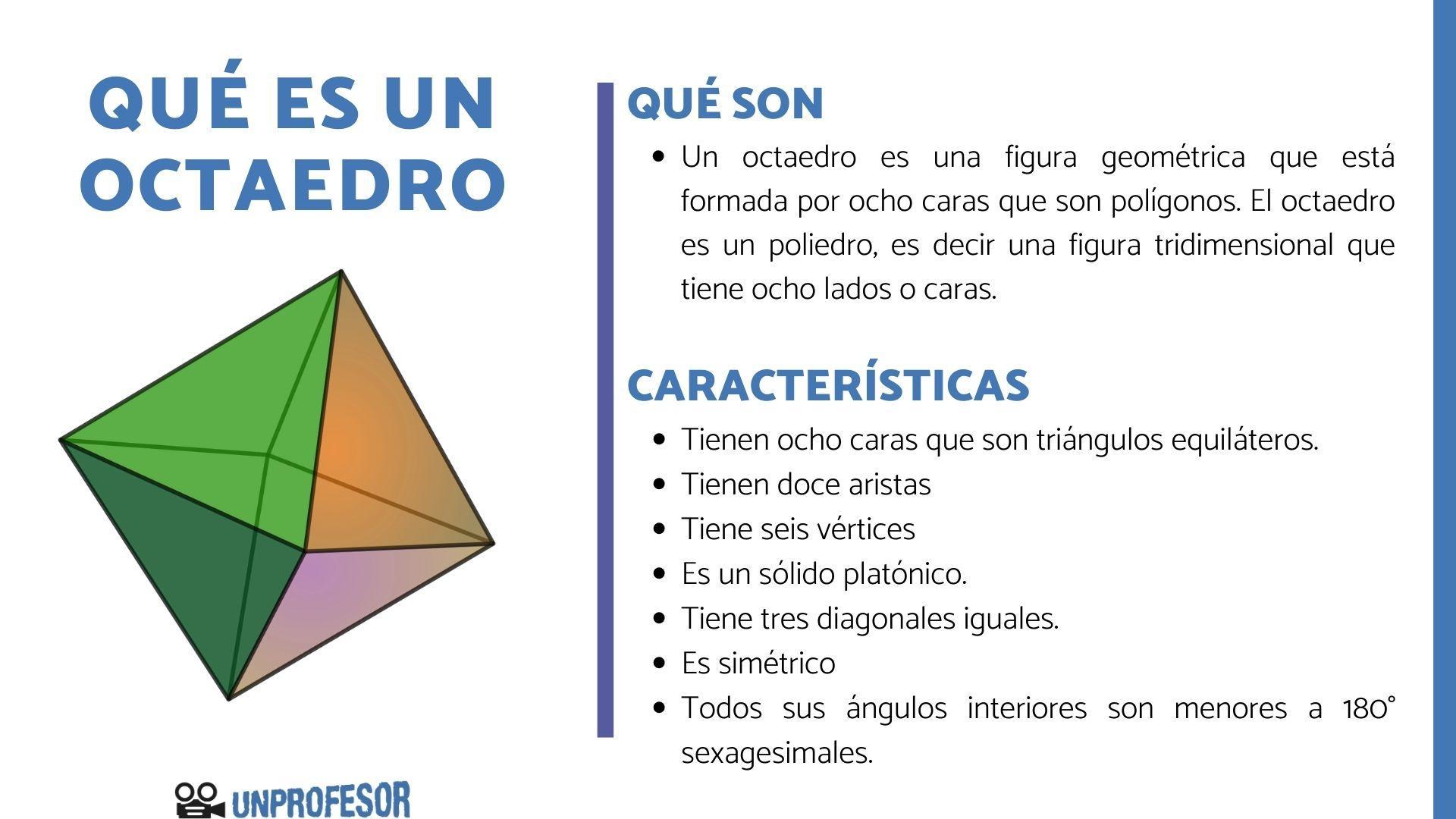
En geometría, un octaedro es aquella figura tridimensional que posee ocho caras en la cuál cada una de ellas es un polígono.
Un octaedro es un poliedro. Recordemos que un poliedro es una figura geométrica de tres dimensiones que está formada por diferentes caras que son polígonos. Mientras qué un polígono es un figura geométrica de dos dimensiones que se construye a partir de segmentos de recta que se unen para formar un lugar o espacio del plano cerrado.
Las caras o lados de un octaedro, es decir los polígonos que lo forman pueden ser, triángulos, cuadrados, pentágonos, hexágonos y heptágonos, es decir cualquier polígono que posea menos de ocho lados o segmentos de recta.
Características de un octaedro
Los octaedros pueden ser regulares, y esto se debe a que están formados por ocho triángulos que son equiláteros, o sea que todos los lados del polígono son iguales. El octaedro regular se ve como la unión de dos pirámides a partir de sus bases. Por lo tanto tiene ocho caras, tiene doce aristas y seis vértices. A este tipo de octaedros se lo denomina sólido platónico. Existen cinco cuerpos considerados dentro de este grupo y son el cubo, tetraedro, octaedro, dodecaedro e icosaedro.
La característica principal de estos sólidos platónicos es que son poliedros regulares y convexos. Es decir, que están formados por polígonos que son todos regulares o iguales entre sí, y que siempre podemos unir dos puntos con una línea dentro del poliedro.
Los octaedros irregulares son aquellos poliedros que poseen ocho caras pero que NO son iguales entre sí y tampoco tienen ángulos iguales. La cantidad de caras que tiene un octaedro irregular puede variar, pero el número siempre será uno PAR.
Como característica, un octaedro que es irregular siempre tiene ocho vértices y doce aristas. Es decir como cualquier octaedro, a parte de poseer ocho caras tal y como su nombre lo indica.
Para saber cuántas caras posee uno de estos poliedros, únicamente podemos contarlas. Depende no sólo de la forma que tengan los polígonos que lo forman sino también del tamaño que tengan cada una de ellas.

Pasos para calcular el área de un octaedro regular
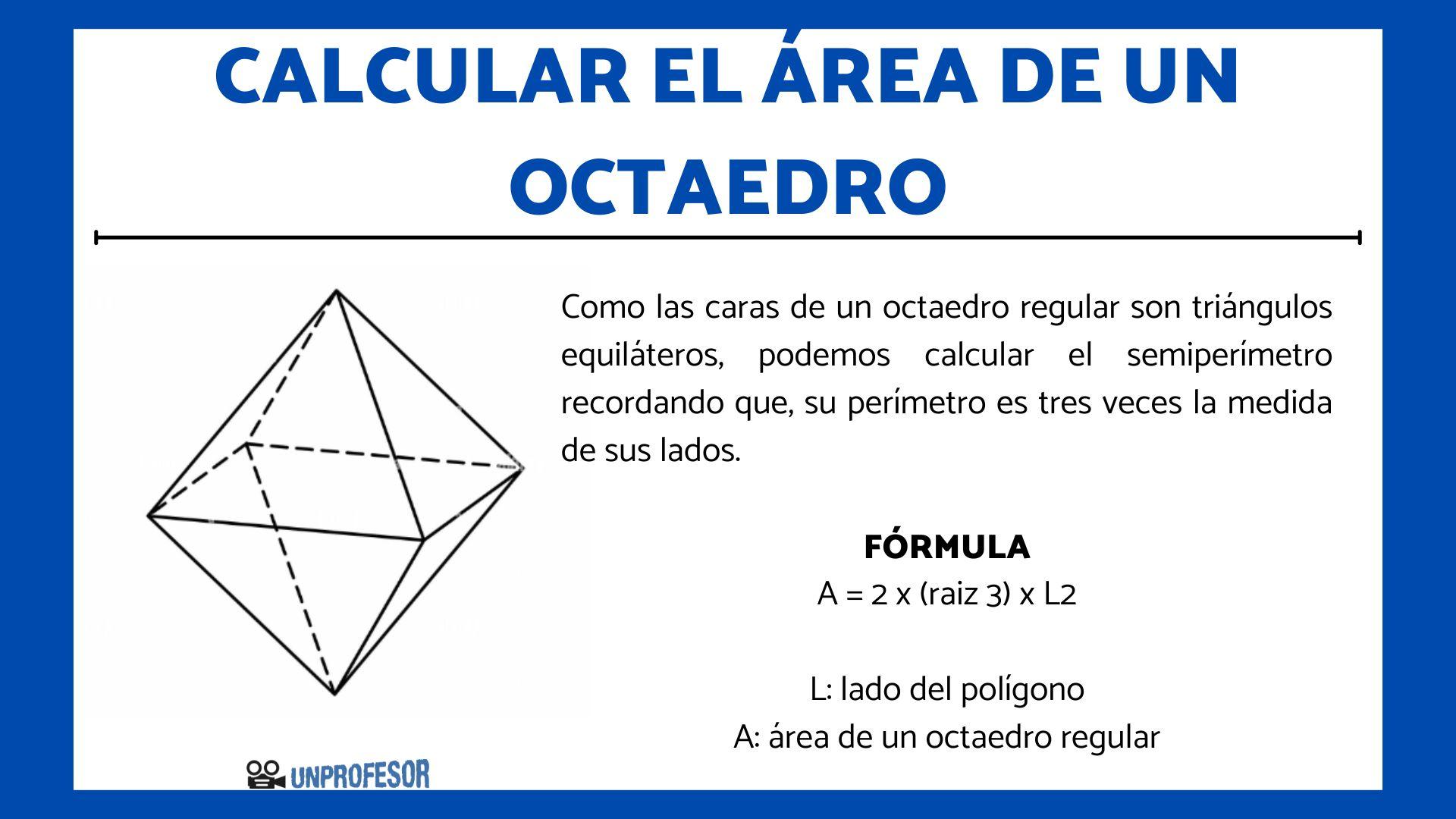
Para calcular el área de un octaedro, debemos calcular la suma de las superficies de las ocho caras que posee. Por lo tanto, podemos calcular el área de un octaedro que es regular igualando el cuadrado de la arista de un octaedro por dos veces la raíz del número tres.
Como las caras de un octaedro regular son triángulos equiláteros, podemos calcular el semiperímetro recordando que, su perímetro es tres veces la medida de sus lados. La fórmula del área del octaedro entonces, queda de la siguiente manera:
A = 2 x (raiz 3) x L2
- L: lado del polígono
- A: área de un octaedro regular
Ejemplos
Queremos calcular el área de un octaedro cuya arista mide 15 m.
Comenzamos entonces. Cada lado del polígono, mide 15 m. Entonces:
- A = 2 x (raiz 3) x L2
- A= 2 x (raiz 3) x 152
- A = 779.42 m2
Por lo tanto el área de un octaedro de arista 15 cm es igual a 779.42 m2

Elementos de un poliedro
Los elementos de un poliedro son:
- Caras: las caras de un poliedro son los lados que forman al mismo, y son ocho polígonos.
- Aristas: las aristas son aquellos segmentos de recta que se unen al juntar dos de las caras de un poliedro.
- Vértices: los vértices son los puntos en los cuales se unen las aristas antes mencionadas del poliedro.
- Ángulo diedro: es el ángulo que se forma en la unión de existe entre las dos caras de un poliedro.
- Ángulo poliedro: es el ángulo que se forma entre aquellos lados que van a coincidir en un vértice.

Ejercicios para calcular el área de un octaedro
Para concluir esta lección sobre cómo calcular el área de un octaedro, vamos a dejarte algunos ejercicios con soluciones para que puedas practicar en casa.
- Calcular el área de un octaedro de arista 5 cm.
- Calcular el área de un octaedro de arista 76 cm.
Soluciones
- Cada arista mide 5 cm, por lo tanto L= 5 cm
- A = 2 x (raiz 3) x L2
- A= 2 x (raiz 3) x 52
- A = 86.6 cm2
Por lo tanto el área de un octaedro de arista 5 cm es igual a 86.6 cm2
2- Cada arista mide 76 cm, por lo tanto L= 76 cm
- A = 2 x (raiz 3) x L2
- A= 2 x (raiz 3) x 762
- A = 69312 cm2
Por lo tanto el área de un octaedro de arista 76 cm es igual a 69312 cm2
Si esta lección te gustó, compártela con tus compañeros. Y recuerda que puedes seguir navegando en la página. En la web de unProfesor hay contenido muy interesante que puede serte útil.
Si deseas leer más artículos parecidos a Cómo calcular el área de un octaedro, te recomendamos que entres en nuestra categoría de Geometría.